
Marc Dupuis GéniSim Inc. 3111 Alger St., Jonquière, Québec, Canada G7S 2M9 A. Koshie, V. Janakiraman Indian Aluminium Company, Limited Hirakud - 768 016, Dist. Sambalpur Orissa, India a.koshie@indal.co.in
S. Karthikeyan, D. Saravanan Confederation of Indian Industry 35/1, Ahiramapuram, 3rd Street, Alwarpet, Chennai - 600 018, India s.karthikeyan@ciionline.org
ABSTRACT
In the present study, the heat balance of the Hirakud smelter aluminium reduction cell has been accurately assessed using only a surface thermocouple and a pyrometer. As it is well known that using a single linear or quadratic relationship to estimate the heat flux from the measured surface temperature does not provide the accuracy required to close the cell heat balance, this approach was not used in this study.
Instead, the fundamental natural convection and radiation heat flux equations were used systematically for each measurement point. Practically, this means that the ambient air temperature and at least one ambient radiative temperature must also be known in addition to the surface temperature for each measurement point. Sometimes, the radiative heat flux could not be accurately estimated using a single ambient radiative temperature. In those cases, a more accurate estimation based on two ambient radiative temperatures and corresponding view factors has been used instead.
It turns out that although at least three temperature measurements are required to estimate a single heat flux, it takes a lot less time to make those temperature measurements using a pyrometer than directly measuring the heat flux using an expensive heat flux meter. Furthermore, no loss in accuracy was detected when using this approach as the cell heat balance could be closed within 5%, the level of accuracy typical of cell heat balance assessment using heat flux meter.
INTRODUCTION
In his paper "Pot Heat Balance Fundamentals", Bruggeman [1] wrote as introduction: "The heat balance is not only a focal point for the economics of production, but also for the science of aluminum production". He also added: "By the end of the 1960's, correlation and simple mathematical models harnessing the power of early computers were available to improve cell design. Since then, both measurement methods and models have advanced further to the point where, new designs are not considered without rigorous testing and screening using these sophisticated tools".
So obviously, the first priorities of the Hirakud smelter cell retrofit program has been to measure the cell heat balance and to develop reliable mathematical models. The present paper focuses on the work done to assess the thermal balance of the cell.
THE CELL HEAT BALANCE
The concept of the cell heat balance is quite simple. Of the total electrical power fed to the cell, less than half is actually used to produce aluminium. The remaining part must be dissipated as heat losses by the cell in order for it to maintain its thermal equilibrium. Experimentally, a cell voltage break down is required in order to calculate the cell internal heat i.e. the heat that the cell needs to dissipate to maintain its thermal equilibrium. In turn, this can be experimentally confirmed by directly measuring the cell heat losses. If the cell heat losses correspond to the calculated cell internal heat, those measurements can be used with confidence in order to calibrate the mathematical models of the cell.
HEAT LOSSES MEASUREMENT METHODS
In general, cells loose heat by natural convection and by radiation. The equations that describe the physics of those two heat transfer mechanisms are well known. In the early cell heat balance measurement campaigns, those equations were indirectly used to compute the heat fluxes on the different cell surfaces and hence to compute the total cell heat losses [2]. They were only used indirectly probably because of the limitation of the computing power at that time: the fundamental equations were used to correlate the different cell surface temperatures to the heat fluxes (see Figure 1 extracted from [2]). Those correlations were established in preparation for the actual field measurement campaign in order to reduce it to the measurement of the cell surface temperatures only. This approach turned out not to produce very accurate results.

Figure 1 - Relation between surface temperature and heat dispersion (Fig 6 in [2])
Very recently [3], those same fundamental equations have been presented again as background theoretical knowledge, but the authors carefully specified that: "Due to geometry and other conditions of an electrolysis cell, (those) equations cannot be used directly for (calculating) the heat flow from shell wall to air".
In [1], Bruggeman clearly expressed the current conventional wisdom of the industry by specifying that heat flux transducer must be used to carry out cell heat loss measurement campaigns. He even pointed out that: "Haupin developed a heat flux transducer especially for pot measurements". Apart from Alcoa, most of the rest of the industry is rather using commercially available heat flux transducers (see Figure 2).

Figure 2 - Commercially available heat flux transducers (www.kyoto-kem.com)
Unfortunately, commercially available heat flux transducers are fairly expensive and relatively fragile. They are also characterized by a fairly long response time of around 10 minutes. This means that cell heat balance measurement campaigns using heat flux transducers are fairly long and expensive to carry out. For that reason, the challenge posed to the authors was to find an accurate way to assess the Hirakud cell thermal balance using only temperature measurements.
FUDAMENTAL HEAT FLUX EQUATIONS
The general form of the heat transfer equations have been published multiple times, references [2,3] being two examples. But as the natural convection heat loss equations are semi-empirical, there exact form varie from author to author. In the present work, we used the following equations to compute the heat fluxes [4]:

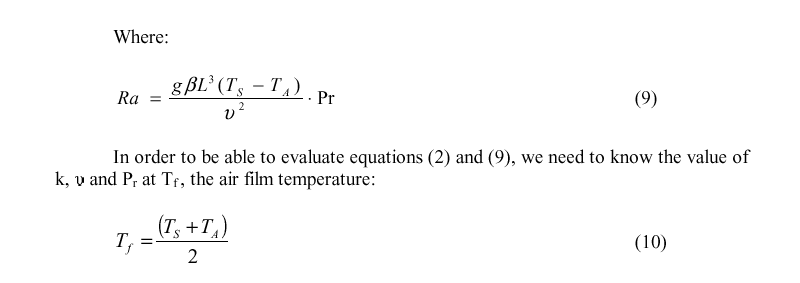
Those air properties are presented in Table 1 [4]:

Finally, by fitting the data of Table 1 with 4 order polynomials, we can establish the following equations for the air thermal conductivity, the air cinematic viscosity and the air Prandtl number respectively:

MEASUREMENT CAMPAIGN
In order to calculate the global cell heat losses, approximately 200 surfaces must be established around the cell. The area of each of those surfaces must be calculated in order to be able to, in turn, calculate the heat dissipated by each of them:
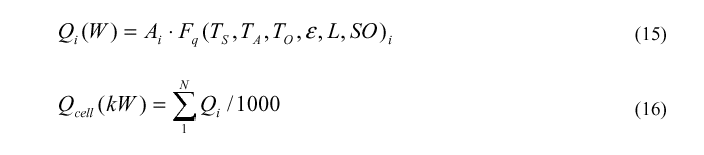
The actual implementation of this approach is not as complex as it may look. It is quite easy to evaluate ahead of time A, ε, L and SO for each surface. For a given cell design, once established, the value of those items will not change. This leaves only three temperatures to be measured per surface TS, TA and TO during the measurement campaign.
In comparison, in a "standard" measurement campaign using heat flux transducers, only qtot is measured for each surface. Yet, measuring TS and TO with a small hand held pyrometer and TA with a thermocouple and a small hand held multimeter is far less cumbersome and requires far less time than using slow to response heat flux transducers connected by wires to an expensive and delicate heat flux meter!
ANALYSIS OF THE RESULTS
Despite all the theoretical and advance preparation work, there were no guarantees that this new measurement approach would produce accurate results. In fact, our first attempt did not; the measured heat losses significantly exceeded the calculated cell internal heat!
Analysis of the results revealed that we were overestimating the heat flux of some very hot surfaces for which the radiation term became very large. Of course, we knew that the radiative exchanges around a cell are very complex and that considering that each surface is only seeing one background radiative temperature could well turn out to be an unrealistic over-simplification. Our first results confirmed that this was the case, at least for some critical surfaces.
This led us to consider that those surfaces are seeing two background radiative objects that are not at the same temperature. Of course, this in turn introduce the need to calculate the view factors for each object:
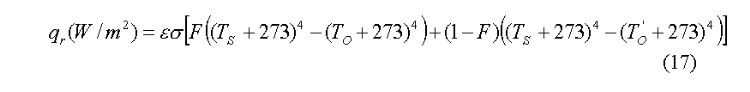
In a second attempt, we use this new equation to evaluate the radiative heat transfer of the few regions of the cell were hot surfaces are partially seeing another hot surface. This second time, the percentage of closure was in the acceptable rage as we can see in Table II. A third attempt, which was also successful, on a different cell confirmed that we had developed an accurate method to assess the thermal balance of the Hirakud cell using only temperature measurements.
Table II

REFERENCES