SHELL DESIGN TECHNIQUE CONSIDERING THE SODIUM SWELLING PHENOMENA OF CARBON CATHODE BLOCKS
Ghasem V. Asadi and Marc Dupuis Alcan International Limited, Arvida Research and Development Centre Jonquière, Quebec, Canada G7S 4K8 Imad Tabsh Compusim Inc. 1003-D 55th Avenue N.E. Calgary, Alberta, Canada 72E 6W1
ABSTRACT
The force generated by cathodic swelling, due to sodium penetration in the carbon blocks on the sides of a cathode shell of an aluminum reduction cell, is not only a function of the size of the cathode blocks but also of the structural strength of the shell.
To analyze this effect and demonstrate its impact on the mechanical shell design, a numerical method was developed to calculate the maximum value of the internal forces in an aluminum reduction cell. The method considers the carbon blocks fully saturated with sodium and, through an interactive technique, calculates the magnitude of the force between the cathode shell and the cathode carbon blocks as well as the deformation and stress distribution of the cathode shell. This method is capable of calculating the plastic deformation of the shell structure. This new interactive method was used successfully to examine a quarter of a cathode shell and gives us the possibility of calculating the internal pressure and deformation of complete cathode shells.
This analysis is performed by means of the Finite Element method and specifically the commercially available software ANSYS is employed. The advanced computation techniques can present the shell deformation and stress development in an animated form.
INTRODUCTION
An aluminum reduction cell is composed of cathode and anode carbon blocks; the cathode carbon blocks rest in a steel shell. The main role of a steel shell is to prevent deformation of the cathode blocks and withstand the forces induced by thermal and chemical changes in the reduction cell. The average life for an aluminum reduction cell varies from 1500 to 3500 days; during this operational period the reduction process performed in the molten bath causes penetration of sodium into the carbon cathode blocks. A consequence of sodium penetration into cathode carbon blocks is swelling of the carbon and expansion of the blocks. This cathode expansion exerts an internal force on the steel shell, which causes its deformation; the steel shell structure enforces the reaction force on the cathode blocks, which reduces the expansion of the carbon blocks due to sodium penetration. In practice these action and reaction forces reach an equilibrium where the steel shell is deformed to a certain extent and the cathode blocks are deformed less than they would do in the free state. It can be seen that the strength of the shell structure plays a major role in the expansion of the carbon blocks and final deformation of the steel shell. A relatively weak shell, which induces a lower reaction force, largely deforms due to the sodium swelling of carbon blocks, consequently it either exhibits permanent deformation or rupture of the shell and failure of the reduction cell.
A well-designed shell is supposed to withstand the internal pressure of the reduction cell and preferably deform in the elastic range of the steel without performing plastic and consequently permanent deformation. On the other hand the steel shell should not be overdesigned by selection of a heavy and complicated structure, as the initial materials and welding costs are essential parameters. To achieve a well-designed structure, magnitude of the forces on the shell structure should be determined through an interactive method which relates the dimensions of the cathode carbon blocks and the shell and also the material properties of the carbon and steel. This interactive arrangement can be employed to determine deformation and level of nduced forces on a specified shell design for a long period of cell operational life.
DESCRIPTION OF THE MODEL AND NUMERICAL ANALYSIS
In 1974 E. Dewing [1] showed that expansion of a carbon specimen due to sodium diffusion is reduced as the restraining force on the carbon is increased. He expressed the stress-strain relationship for sodium swelling of carbon as:
e = eo 10^ks (1) Where e is the carbon strain at equilibrium eo is the carbon free expansion strain, i.e. no restraint s is the compressive stress in the carbon k is a constant
This relation is employed in a numerical model to calculate the magnitude of the exerted force on the walls of a cathode shell; the exerted force deforms the shell to a certain extent, and returning to the Equation (1) the force at each point of the shell at the new position is calculated and compared with the nodal force on the structure; if these two values are not equal (within a certain tolerance) the iteration will continue. From the structure side, when the stress level exceeds the elastic limit of the steel, a plastic analysis will start and equilibrium of the structure would be calculated considering the plasticity of the structure. Following the above logic the final shape of the shell and stress distribution along it is calculated.
In 1992 Dupuis, et al. [2] reported the development of this technique and demonstrated its application to a slice of a potshell. This work has been continued and expanded to a more powerful tool which is now capable of handling a quarter of the shell, calculating the pressure distribution on the end and side walls and also predicting the deformation of the walls.
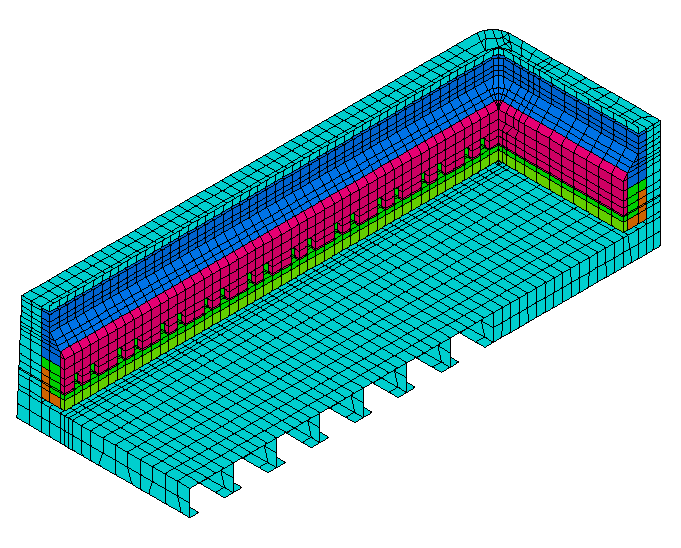
This work as well as that reported in [2] is developed employing the commercially available software ANSYS [3] using the parametric design language (APDL) capability of the program. A mathematical model for a quarter of the potshell is developed using the shell elements and a pier is modeled by the 3-D solid element; Figure 1 shows a model for the shell and the pier. Symmetrical boundary conditions are defined for the two sides of the model to present two axes of symmetry of the potshell. The developed model is run in an iteration loop which is shown in Figure 2.

Figure 1: Model of a quarter of a shell with wall piers
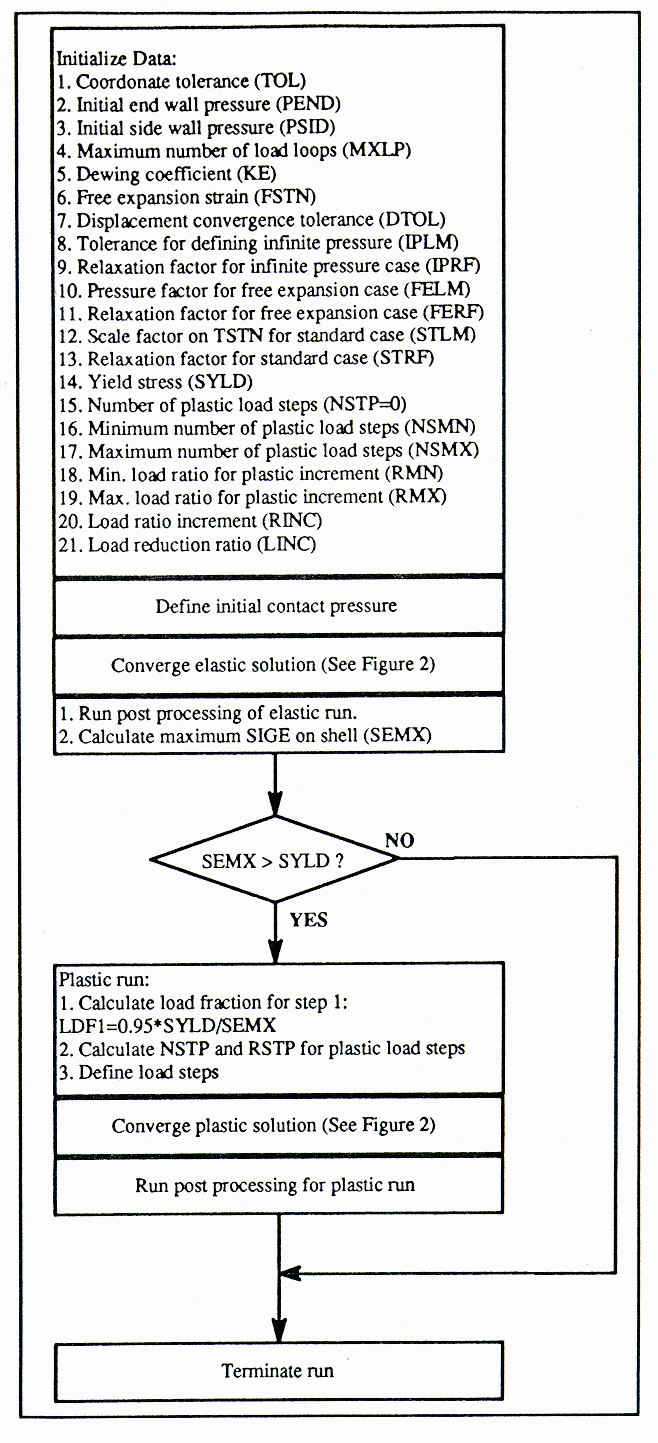
Figure 2: Main processing logic
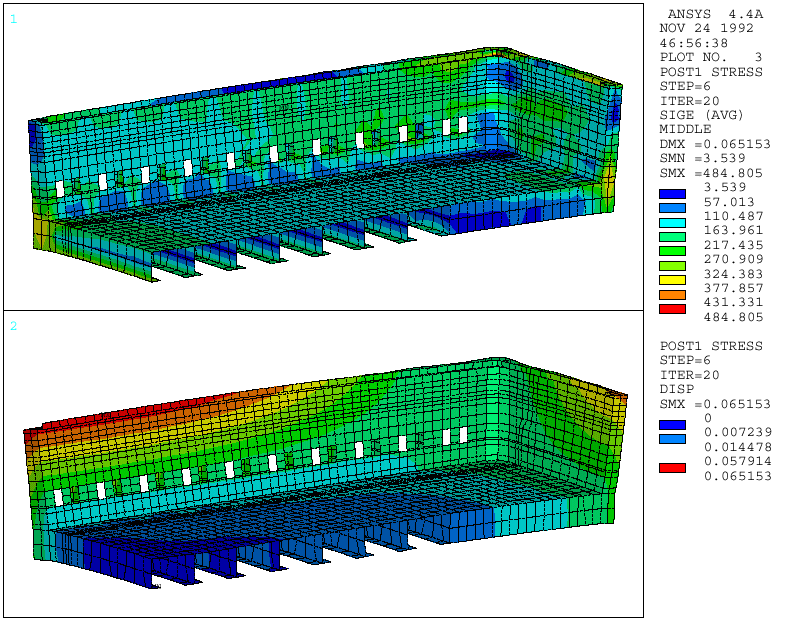
Figure 3: Stress distribution and deflection of the potshell
This algorithm is applied to an experimental shell; the wall deflection, stress distribution along the shell and pressure distribution on the pier are calculated. Figure 3 shows the stress distribution along the pot-shell; it shows that the maximum stress is 484 MPa in a very localized region in the corner. The maximum stress in the cradle is lower at about 370 MPa. This figure also shows that maximum deflection of the middle of the side wall is 65 mm and in the middle of the end wall is about 40 mm. Figure 4 shows measured deflection of the side and end walls of the potshell. Comparison of the measured data with the calculated results shows a very good agreement of the two values.
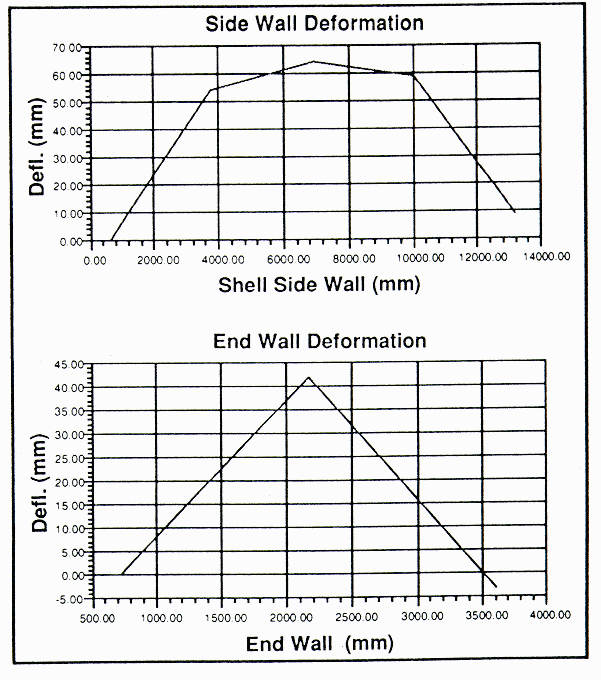
Figure 4: Measured deflection of the side and end wall of the potshell
Figure 5 shows the pressure distribution on the contact face of pier and cathode blocks; it shows that the maximum pressure is induced at the region close to the corner and specially along the end wall; the maximum level of pressure calculated in this analysis is 21.8 MPa at the corner. This level of pressure between the carbon blocks and the pier seems to be too high to be withstood by either pier or the carbon blocks. To point out the reason for this high level of pressure a series of experiments is needed to verify the stress-strain relationship in carbon due to sodium swelling.

Figure 5: Contact pressure distribution on the pier surface
CONCLUSIONS
With the present method we are in a position to design a new potshell or to revise the structural design of any of our potshells without guessing the magnitude of the internal pressure. This method can be considered as one step ahead in the design of aluminum reduction potshells. To increase the accuracy of this method, more tests should be done on the sodium swelling phenomena of carbon blocks and the relationship of the carbon expansion with the magnitude of the applied pressure on the carbon block should be verified.
REFERENCES