|
Abstract
In the present study, a full 3D cell-cathode thermo-electric model of a 500 kA demonstration cell has been developed.
In parallel, a non-linear transient wave MHD model for the same 500 kA demonstration cell, taking into account the shielding effect of
the optimized geometry of the potshell, has been developed.
Preliminary results of the impact of the interactions between the cell thermo-electric and MHD models are presented.
Introduction
In Part 1 of this collaborative work, the authors developed both a 3D quarter-cell thermo-electric model and a non-linear wave MHD model
of a 500 kA demonstration cell design [1]. The quarter-cell model comprises one quarter of the cell with cathode and anode linked together.
The other three quarters of the cell are present by virtue of symmetry. For details on the design of this 500 kA cell, see the article
published in the magazine Aluminium last year [2].
The present collaborative work is also a direct follow-up of the work presented in 2002 on the tentative development of a 3D full-cell and
external bus-bar thermo-electric model [3]. At that time, a model of a 300 kA demonstration cell design was built but could not be solved
on the PIII computer then available.
The need to link together a 3D full-cell thermo-electric model and the non-linear wave MHD model into a coupled thermo-electric-MHD model
of an aluminum electrolysis cell has already been explained in details previously [4]. The ultimate goal of the current collaborative
work is to develop such a coupled thermo-electric-MHD model which would be one of the steps towards the development of a complete
multi-physics model of an aluminum electrolysis cell.
In this paper, the results of a 3D full-cathode and external bus-bar thermo-electric model are presented. Attempts to calculate
thermo-electric fields in a full-cell and a half-cell model are also discussed. A full-cell model is essentially a full-cathode model
with the anode coupled to it. A half-cell model is one half of the full-cell model, the other half is present by virtue of symmetry.
|
|
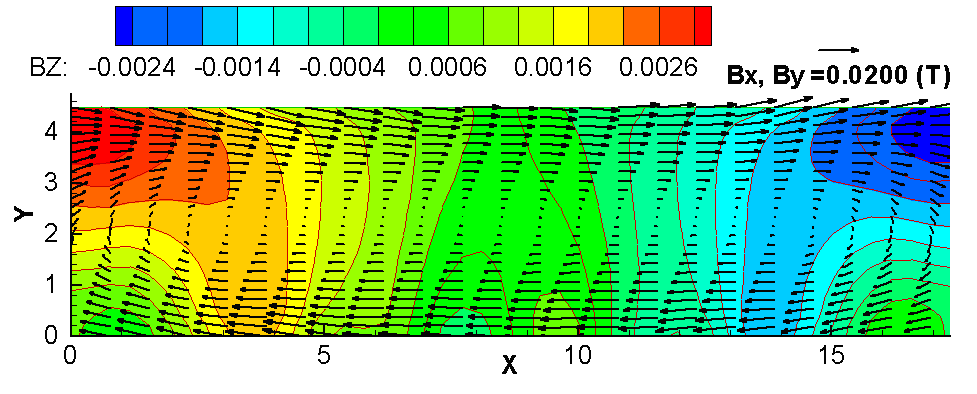
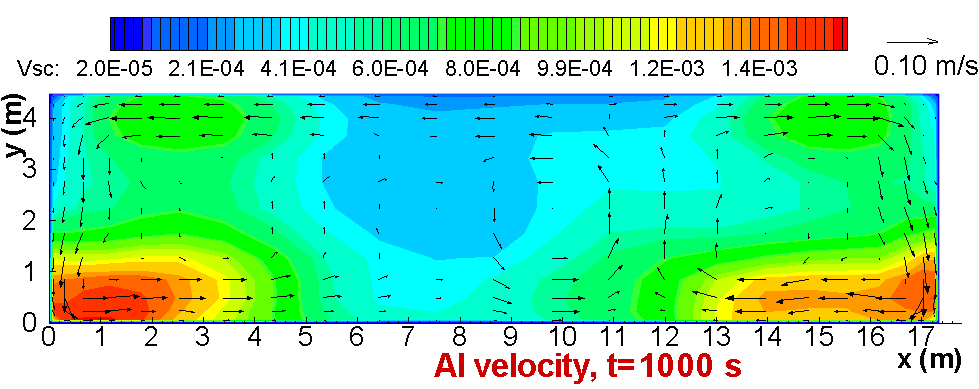
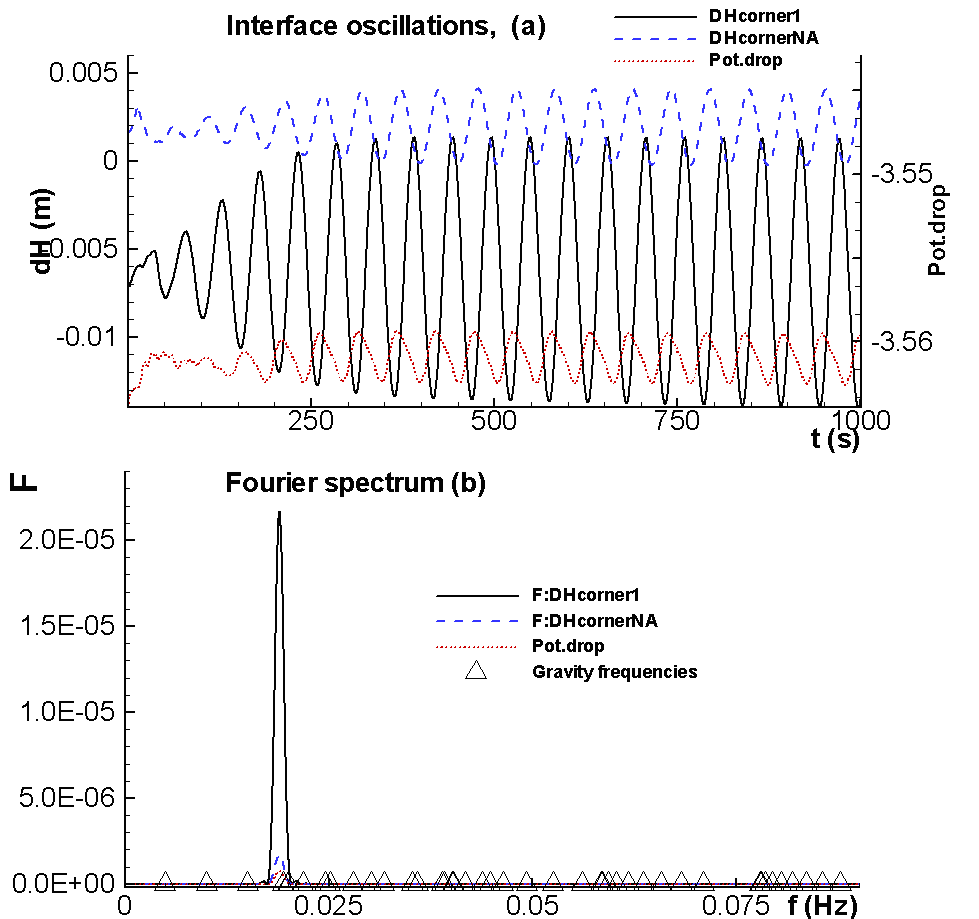
The non-linear wave MHD model is extended to take into account the shielding effect of the detailed and optimized geometry of the potshell.
Finally, the velocity fields calculated in the MHD model are used to define the metal/ledge and bath/ledge local heat transfer coefficients
in the thermo-electric model.
3D full-cathode and external bus-bar thermo-electric model
As demonstrated in [5], in the first approximation, it is not necessary to model in detail the anode panel in order to calculate the
current density in the metal pad when all the anodes are carrying nearly equal current. The position of the ledge, the geometry of the
block/collector bar connection and the external bus-bar design all have more influence on the metal pad current density than small
resistance discrepancy in the anode network. Hence the 3D full-cathode and external bus-bar thermo-electric model is sufficient to
compute the detailed current density in the metal.
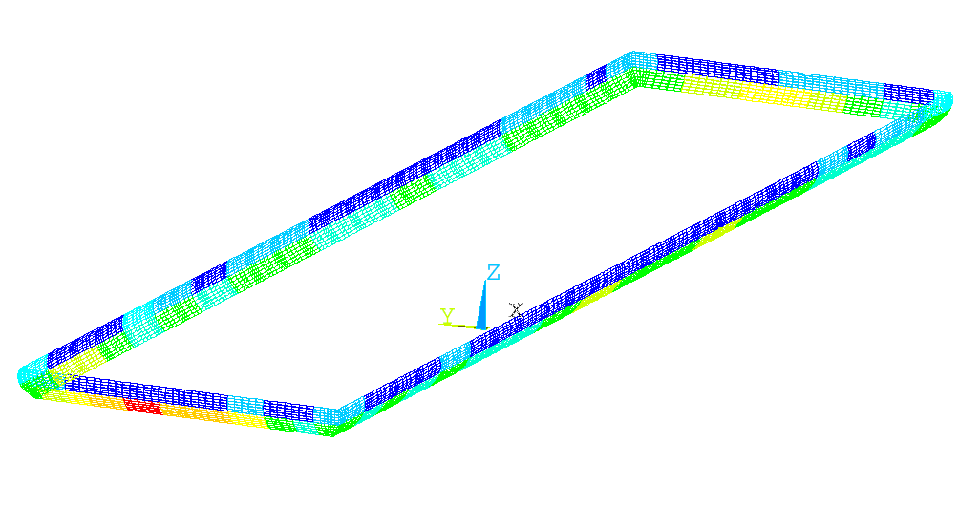
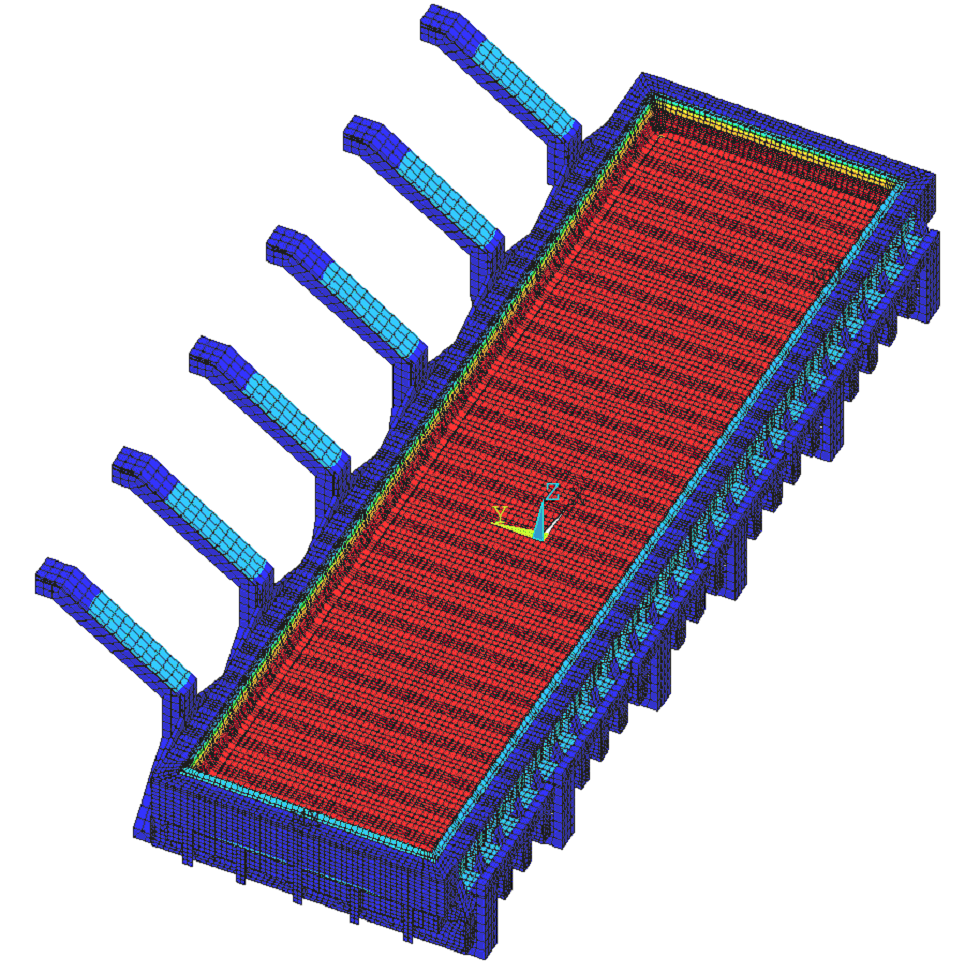
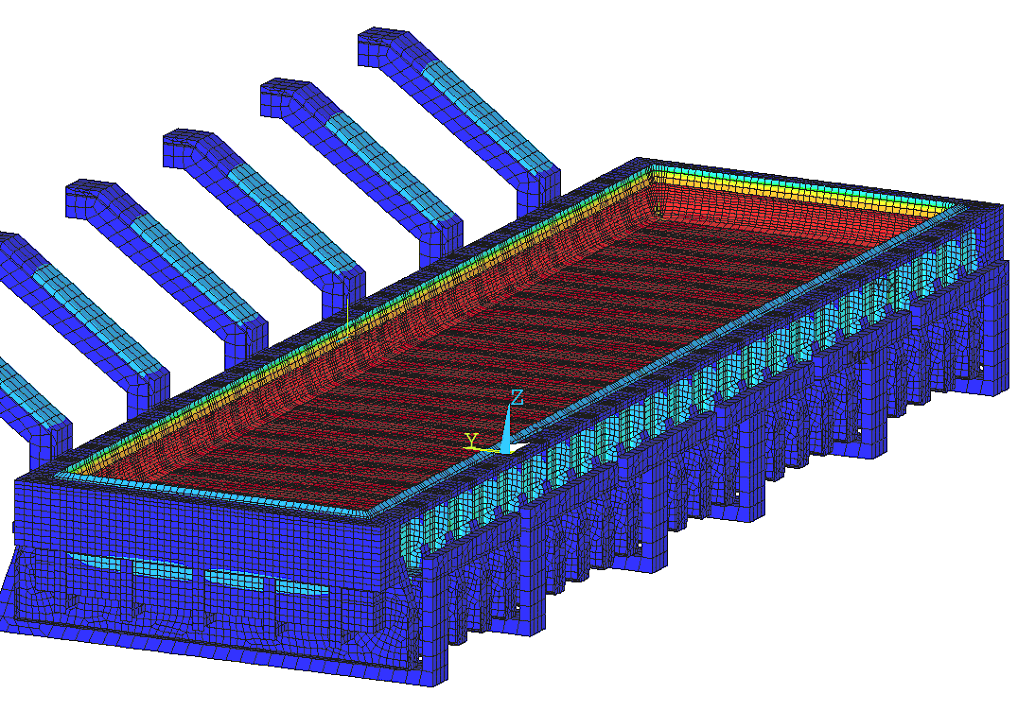
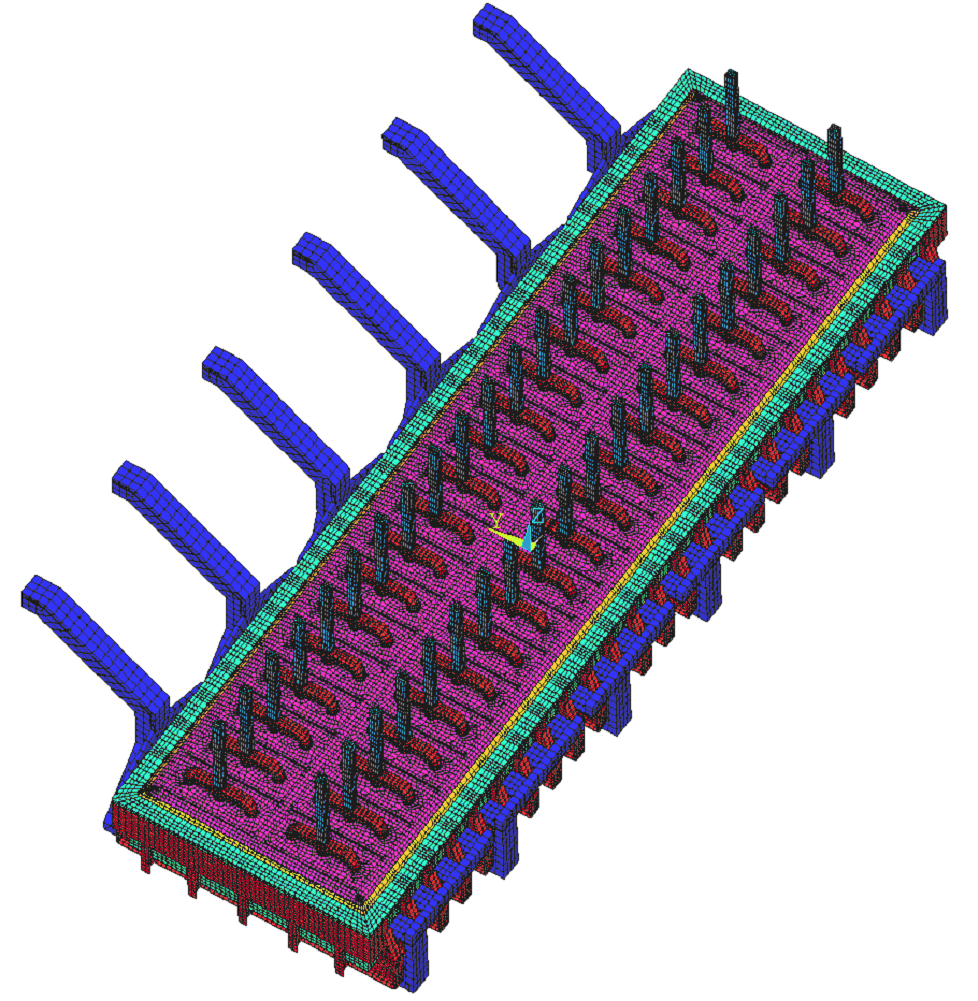
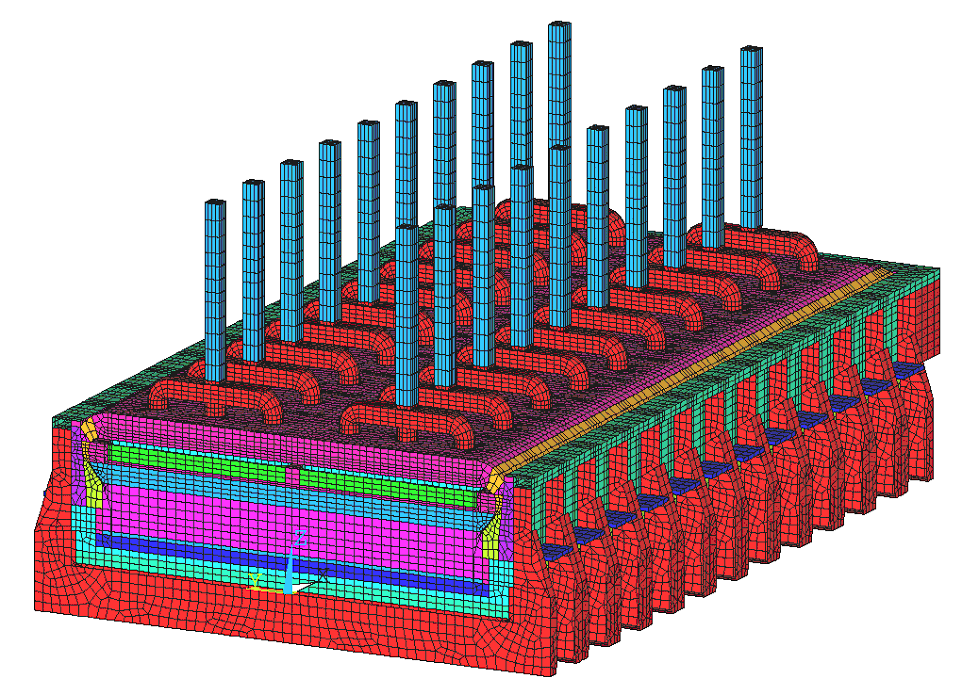
Figure 1 shows the mesh of the 3D full-cathode and external bus-bar thermo-electric model. For the 500 kA demonstration cell, the mesh is
made of 354116 finite elements. Figure 2 shows the distribution of the local heat transfer coefficients at the metal/ledge and bath/ledge
interface for the preliminary run. This distribution is not based on the velocity fields calculated by the MHD model or any other velocity
field. It is rather arbitrarily generated by a sinusoidal function, which gives a variation along the walls, similar to what four flow
pools would give.
A P4 3.2 GHz computer was used to compute the solution. It took 17 CPU hours to solve the model in order to perform 3 loops of the ledge
shape convergence scheme. The convergence scheme was stopped before reaching convergence, as this was not required for this preliminary
run.
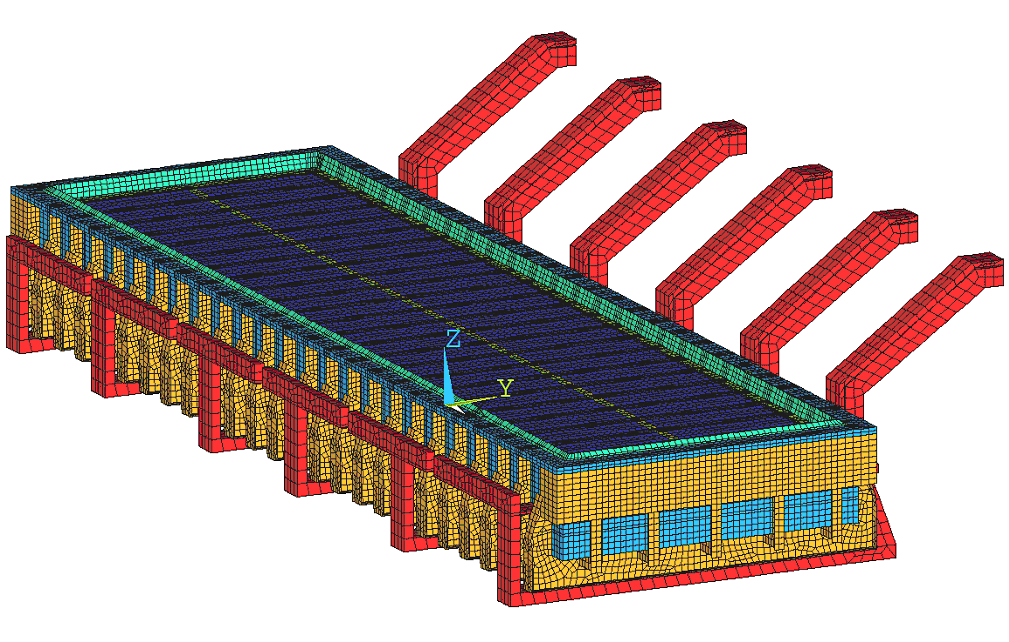
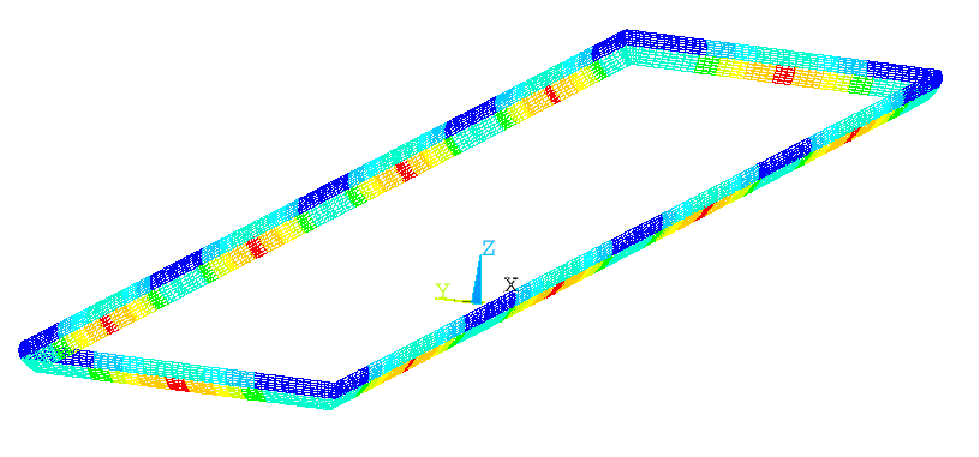
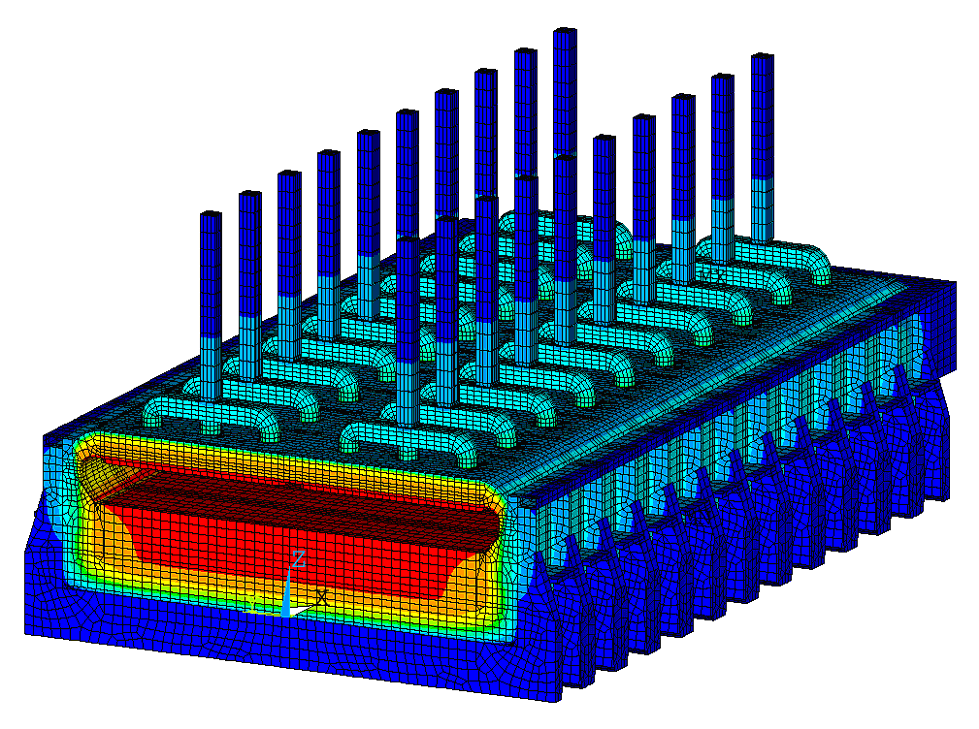
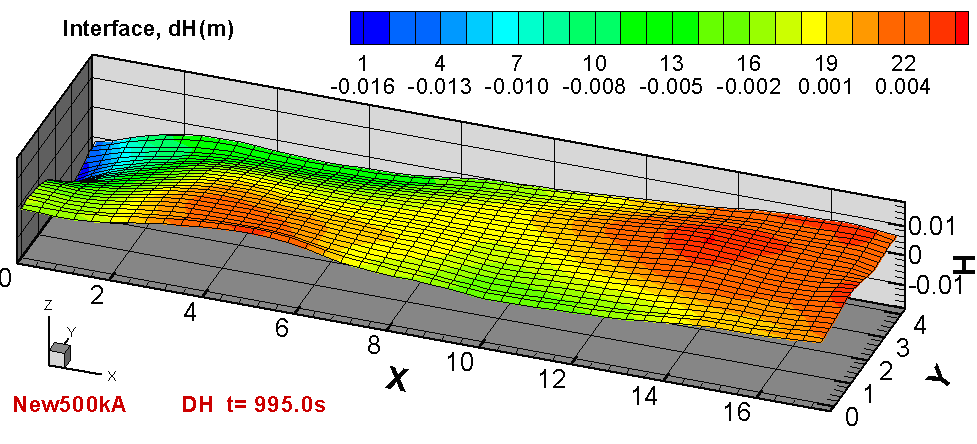
Figure 3 shows the obtained thermal solution, while Figures 4 and 5 show the metal pad voltage solution and the metal pad current density,
respectively. It can be observed that the resulting ledge profile thickness varies along the cell perimeter: the ledge is thicker where
the local heat transfer coefficient was set low and thinner where the local heat transfer coefficient was set high. As a result, the
intensity of the horizontal current in the metal pad is not uniform along the cell but rather varies from cathode block to cathode block
depending particularly on the ledge toe variation along the cell perimeter.
|


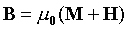
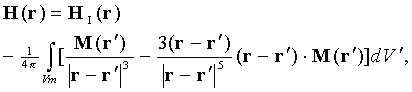


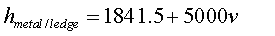 (3)
(3)
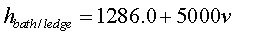 (4)
(4)