| · | Pechiney Continuous Tracking: continuous tracking of the cell pseudo resistance to manage a fixed binary alumina feeding policy mixed with resistance control [11]. |
| · | Demand Continuous Tracking: continuous tracking of the cell pseudo resistance to manage an adjustable tertiary alumina feeding policy mixed with resistance control [12]. |
Validation Exercise
It is clear from the previous discussion that modeling the behavior of a reduction cell is fairly complex. One is left with the question whether it is possible to adequately simulate the process. Hence, thorough validation of the program is critical.
Two levels of validation can be identified. The first ensure that the program performs as it should, i.e. the input data is properly stored and accessed, the equations in the submodels are coded correctly, the control logic and the interaction between events and cell states is properly represented, etc. This level of validation was achieved by running a number of examples designed to test various combinations of features as part of the software quality assurance (QA) program.
The second level looks at a particular cell design and ensures that the program can adequately predict the measured behavior. Successful validation depends on two factors: accurate representation of the cell characteristics; and accurate measurements. The cell characteristics include the geometry, material properties, operational procedures and so forth. It also includes proper selection of the equations that characterize the process.
Aratu 1984 Measurement Campaign
Satisfied with the results of the QA program, the next step was to validate a model of an operating cell. The Aratu smelter, owned by Alcan Brazil, had characterized experimentally the dynamic behavior of their V.S. pots in the early days of the smelter. This data has been used to validate a model of the operating cell.
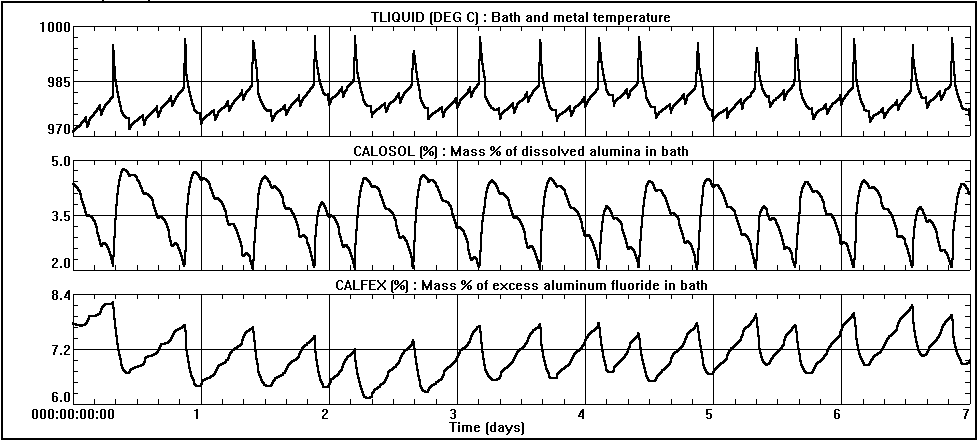
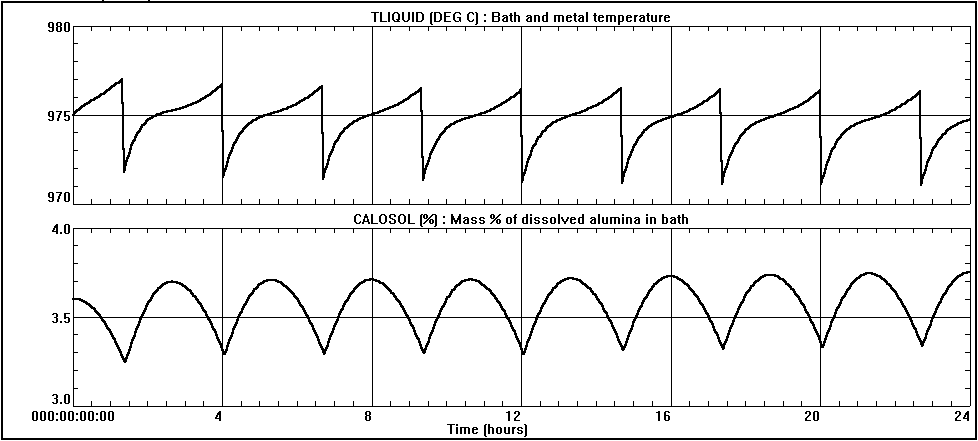
The extensive measurement campaign that was carried out at the time consisted of measuring several data from two pots. These included the bath temperature, the concentration of alumina dissolved in the bath and the concentration of excess AIF3 in the bath. Measurements were taken every hour for a period of 24 hours. The data is presented in figures 1 and 2.
At the time of the measurements, the typical operational characteristics of the Aratu V.S. potline were:
| Amperage | 120 kA |
| Cell voltage | 4.2 V |
| Current efficiency | 89% |
| ACD | 4.3 cm |
| Concentration of excess AIF3 | 8% |
| Average bath temperature | 980 °C |
| Bath level | 19 cm |
| Metal level after tapping | 33 cm |
| Metal tapped each day | 860 kg |
| Alumina feed per break | 125 kg |
| Break frequency | 2 hrs 40 min |
| Alumina feed per anode effect | 250 kg |
| Average anode effect frequency | 2 per day |
| Net anode consumption | 530 kg C/t Al |
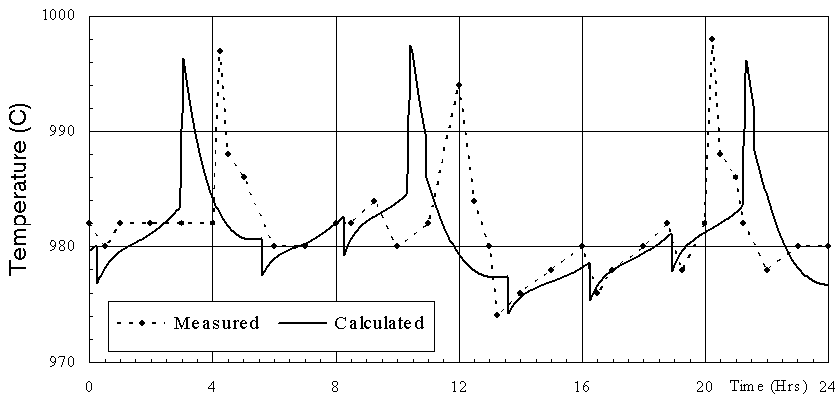
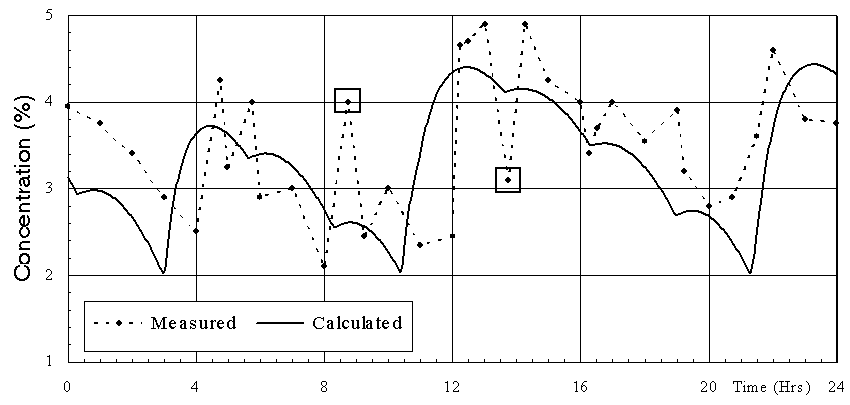
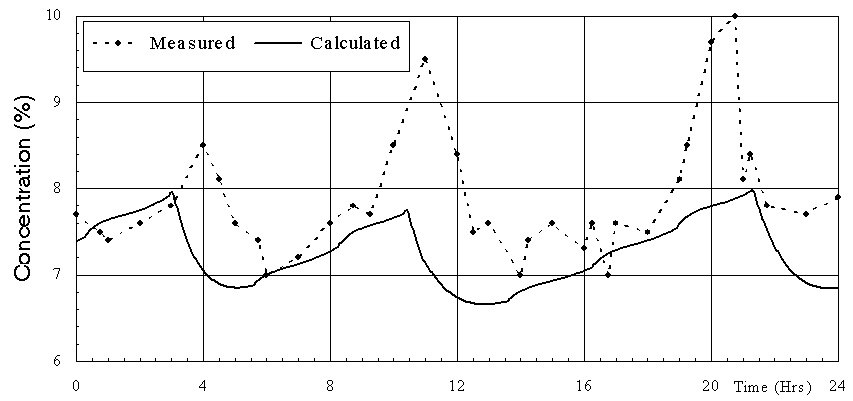
As can be seen in figures 1 and 2, the data obtained is very consistent, showing that the process was well under control during the measurements and that the experimental sampling errors were minimized. Furthermore, the measured behavior compares favorably with the above operational characteristics with the exception of the anode effect frequency. Pot A had 3 anode effects that day while pot B had 4. This discrepancy indicates that the target average break feed of 125 kg was not achieved consistently (other less probable reasons could be poor alumina dissolution or higher current efficiency).
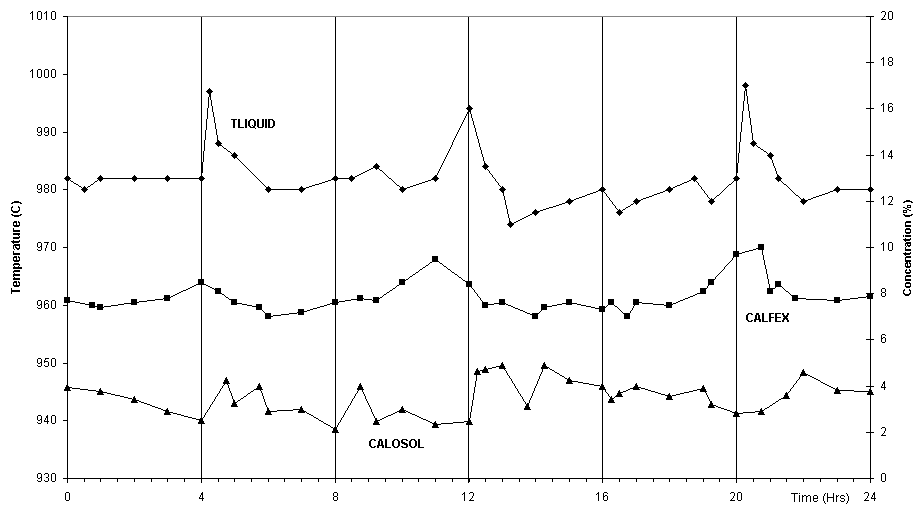
Figure 1: Measurements from Pot A. TLIQUID: bath temperature; CALOSOL: concentration of dissolved Al2O3; CALFEX: concentration of excess AIF3.
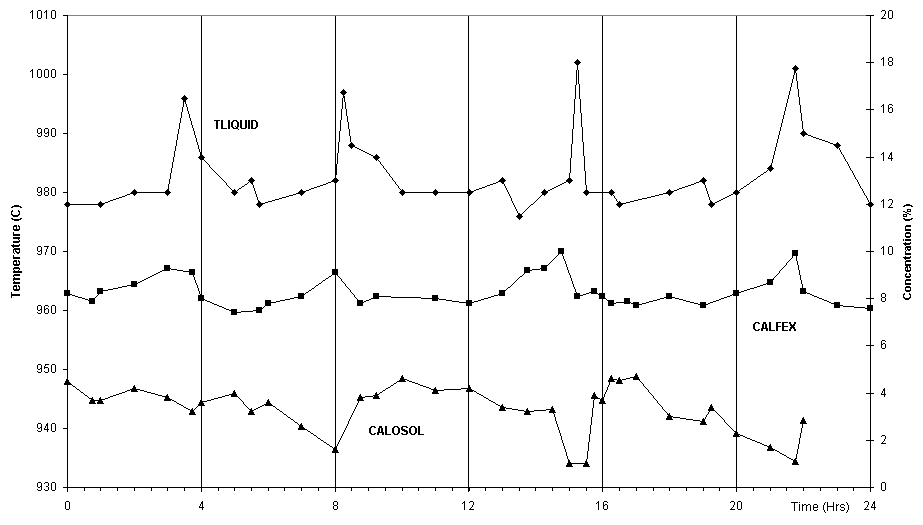
Figure 2: Measurements from Pot B. TLIQUID: bath temperature; CALOSOL: concentration of dissolved Al2O3; CALFEX: concentration of excess AIF3.
Model Results
Data obtained from a thermo-electrical blitz campaign carried out when the measurements were taken along with the cell geometry and operational characteristics were used to define a model of the Aratu pot. Published equations were used in the submodels to characterize the process behavior.
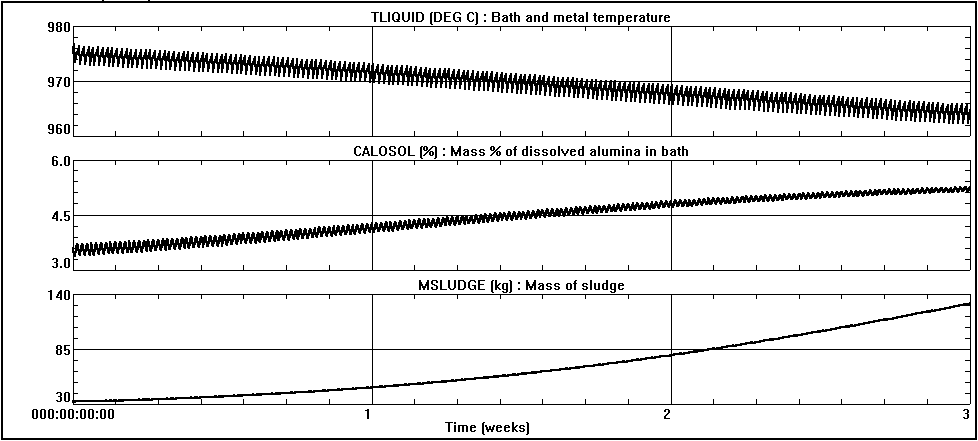
The first step in processing the model was to obtain a steady state solution to start the transient run. It was relatively simple to fine tune the model to closely reproduce the target cell characteristics noted above. Input values (such as the operating temperature, bath chemistry, anode/cathode heat dissipation, etc.) were adjusted within the measured range. Calculated values such as the ACD, current efficiency, cell voltage, etc. are shown in Table II. They compare favorably with the target values.