
Using Mathematical Models to Improve the Thermal Balance of Hall-Héroult Cells
Marc Dupuis GéniSim Inc. 3111 Alger St., Jonquière, Québec, Canada G7S 2M9 email:
ABSTRACT
Two well established reliable and commercially available mathematical tools specially designed to assist the improvement of the thermal balance of Hall-Héroult cells during a retrofit study are being presented.
The first tool, Dyna/Marc, is a Windows-based lump parameters+ steady-state and dynamic model designed to give fast answers to "what if" questions, provide fast trend analysis and produce fast risk assessment analysis by performing Monte Carlo studies.
The second tool is a set of ANSYS-based 3D steady-state finite element thermo-electric half-anode / cathode slice / cathode corner / full cell slice / full cell quarter models that give accurate and detailed predictions of the cell heat balance.
INTRODUCTION
The power consumption of the Hall-Héroult cell being one of the major operating costs, the aluminium industry is constantly trying to reduce the specific power consumption of smelters expressed in kWh/kg of aluminium produced.
Today, best results are:
| 12.9 - 13.0 kWh/kg for high amperage PBF cells | |
| 14.0 - 14.5 kWh/kg for best VSS cells |
Older smelters still operating at 17 - 18 kWh/kg are feeling an increasing pressure from their more efficient competitors. They have essentially two options:
| 1) | Retrofit their cell design in order to improve their power consumption and hence reduce their production costs |
| 2) | Be run out of business |
RETROFITTING EXISTING CELL DESIGNS
Retrofitting a cell design in order to improve its power consumption typically involves improving the cell thermal balance and the cell MHD stability in order to be able to increase the cell amperage (notice that depending on the technology, sometimes it is possible to increase the cell amperage without improving the MHD).
Alternatively, the power consumption can be improved simply by adjusting the cell thermal balance in order to be able to reduce the cell voltage while keeping the same cell amperage. As retrofitting the cell busbar network is a lot more expensive than retrofitting the cell lining design, the return on investment of the second type of retrofit is typically greater.
It is important to point out that for the above two scenarios, improving the cell thermal balance doesn't mean the same thing: in the first case, the cell heat dissipation must be increased while in the second case, it must be decreased.
In fact, improving the cell thermal balance really means adjusting the cell lining design in a way that it is "compatible" with the required level of heat dissipation: a compatible cell lining design being one that will promote the formation of an "appropriate" (neither too thin or too thick) ledge profile while dissipating the internally produced heat (cell internal heat expressed in kW).
USING MATHEMATICAL TOOLS TO IMPROVE THE CELL THERMAL BALANCE
Historically, up to the 70's, the only way to improve a cell conception was to try alternative designs in prototypes. In a way, because the physics of the Hall-Héroult cell is so complex [1], prototypes are still ultimately relied on to test proposed cell designs. Yet, it is now possible to drastically reduce the number of physical prototyping trial and error design loops by using mathematical models to perform most of that trial and error development work using virtual prototyping instead.
As physical prototyping takes a lot of time and is quite expensive, the possibility to be able to use mathematical models to actually do most of the trial and error development work is a huge advantage. But of course, to be able to do so, reliable mathematical models must be available!
INVESTING IN THE DEVELOPMENT OF MATHEMATICAL MODELS: FINANCIAL RISKS AND REWARDS
The Hall-Héroult process being so complex on one hand and the measurement of the process behavior being so difficult to perform on the other hand, the development of reliable Hall-Héroult cell mathematical models was, and continues to be a real challenge. This means that it is a risky R&D activity that does not offer any real guarantee of success.
As previously presented [2], things basically can go wrong the two opposite ways:
| 1) | The development of a "quick and dirty" model that will not be representative of the real behavior of the process |
| 2) | The never-ending development of a "monstrous" unmanageable model that tries to take everything into account |
Financially, the first type of failure is less damaging as the development of a "quick and dirty" model does not require too much time or investment. Yet, as using unreliable models will lead to the proposal of inappropriate designs, their usage only slows down retrofit projects by increasing rather than decreasing the number of prototypes required to produce a successful design.
The second type of failure can be far more damaging financially, as it implies massive investment in a lengthy R&D program. Sooner or later, typically rather late, the unproductive program will be turned down without having produced any return on that massive investment.
An example of such a program "could" be the R&D activity related to the Alcoa Convex C1 "supercomputer" center [3]. In that program, among other things, ESTER/PHOENICS MHD models were developed. That "supercomputer" center was closed down in the late 80's-early 90's, putting on hold further development/applications of those big models.
On the reward side now, as quoted from Pechiney people themselves, their successful development of the AP18, AP30 and also potentially of the AP50 cell technologies relied heavily on "four pillars" [4]:
| 1) | Magnetic and MHD models |
| 2) | Cell thermo-electric and busbars balance electrical models |
| 3) | Potshell/superstructure mechanical models |
| 4) | Transient thermo-mechanical cell start-up model |
But, as the successful development of reliable mathematical models depends greatly on the possibility to do frequent reality check comparisons, it will also be fair to say that Pechiney success story also relied heavily on the extensive prototyping program that was carried on at the LRF experimental center in St-Jean de Maurienne [5,6].
REDUCING THE FINANCIAL RISK AND SHORTENING THE PAY BACK TIME BY USING WELL ESTABLISHED RELIABLE AND COMMERCIALLY AVAILABLE MATHEMATICAL MODELS
The development of reliable models requires many reality check cycles involving: the selection of a theoretical concept to be implemented in the model, the conversion of the theoretical concept into a numerical scheme, the actual coding and debugging of the numerical scheme and finally the production of numerical results and their confrontation with actual measurements. A model that has been demonstrated to be reliable is then a precious asset.
The possibility to license such models not only eliminates completely the financial risk associated with the R&D activity of developing them, it also drastically reduces the delay between the initial investment and the actual pay back time when a successful retrofit project starts to produce more power efficient pots.
For that purpose, GéniSim Inc. is offering two well established and reliable mathematical tools ready to be used in a retrofit project aiming at improving the cell thermal balance:
| - | Dyna/Marc, a Windows-based lump parameters+ steady-state and dynamic model designed to give fast answers to "what if" questions, provide fast trend analysis and produce fast risk assessment analysis by performing Monte Carlo statistical studies |
| - | ANSYS-based 3D steady-state finite element thermo-electric half-anode / cathode slice / cathode corner / full cell slice / full cell quarter models that give accurate and detailed predictions of the cell heat balance. |
DYNA/MARC LUMP PARAMETERS+ MODEL
Dyna/Marc stands for Dynamic Model of aluminium reduction cell. It is a lump parameters+ model, the meaning of the "+" being described in a paper presented at the TMS conference this year [2]. Dyna/Marc can be used in different contexts. First, it can illustrate the behavior of the Hall-Héroult process in the context of a general purpose aluminium electrolysis training course. As an example, Figure 1 and 2 illustrate the impact of undesirable alumina feeding from the cover material during an anode change on the cell current efficiency.
Dyna/Marc can also be used to test changes to the cell control logic or to train operators using a cell controller. As an example, VAW has developed a custom version of Dyna/Marc called Dyna/Marc-Elas and they use it to train new operators on their Elas cell controller. As another example on the application of Dyna/Marc in that field, Figure 3 and 4 illustrate the impact of changing the bath sampling frequency and the formula that is used to adjust the amount of AlF3 added to the cell on the long-term evolution of the bath chemistry.
As a mathematical tool to improve the cell thermal balance, Dyna/Marc is mostly used in steady-state mode. At the beginning of a retrofit project, it provides fast answers to "what if" questions and can produce trend analysis (see Figures 5 and 6). As explained in [2], at the beginning of a retrofit project, it is more important to have fast rather than very accurate answers.
Later on, the Monte Carlo statistical tool of Dyna/Marc can be used to perform a risk assessment analysis [7] (see also Figure 7). As explained in [7], risk assessment analysis are important because no mathematical model is 100% accurate and often a 5% compound inaccuracy on the main models predictions (anode panel heat loss, anode voltage drop, cathode voltage drop, etc.) can translate into a 25% offset between the average thickness of the ledge at the metal level model prediction and the one measured in the prototype for example. Results of a risk assessment analysis can be used to justify the addition of a safety factor in the proposed design.

Figure 1: Operation with undesirable alumina feeding during anode change
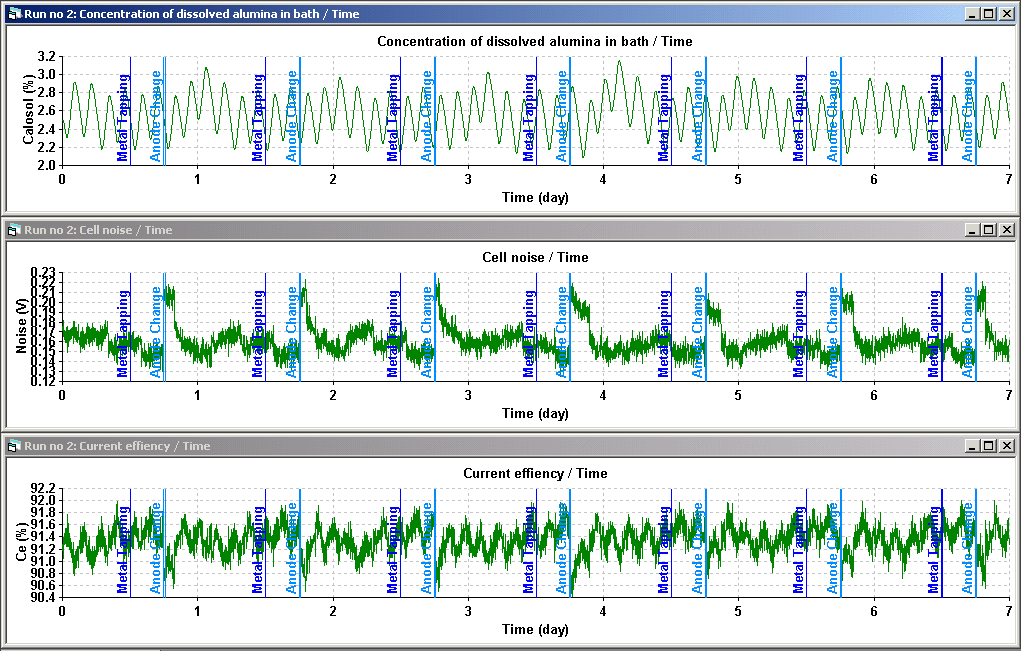
Figure 2: Operation without undesirable alumina feeding during anode change
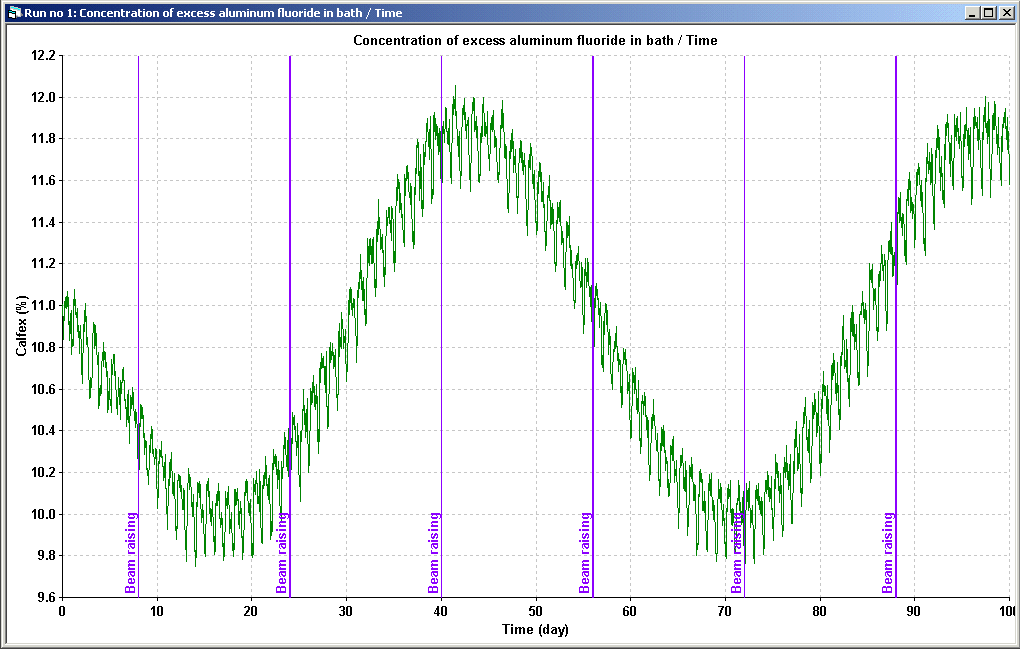
Figure 3: Operation with bath sampling every day
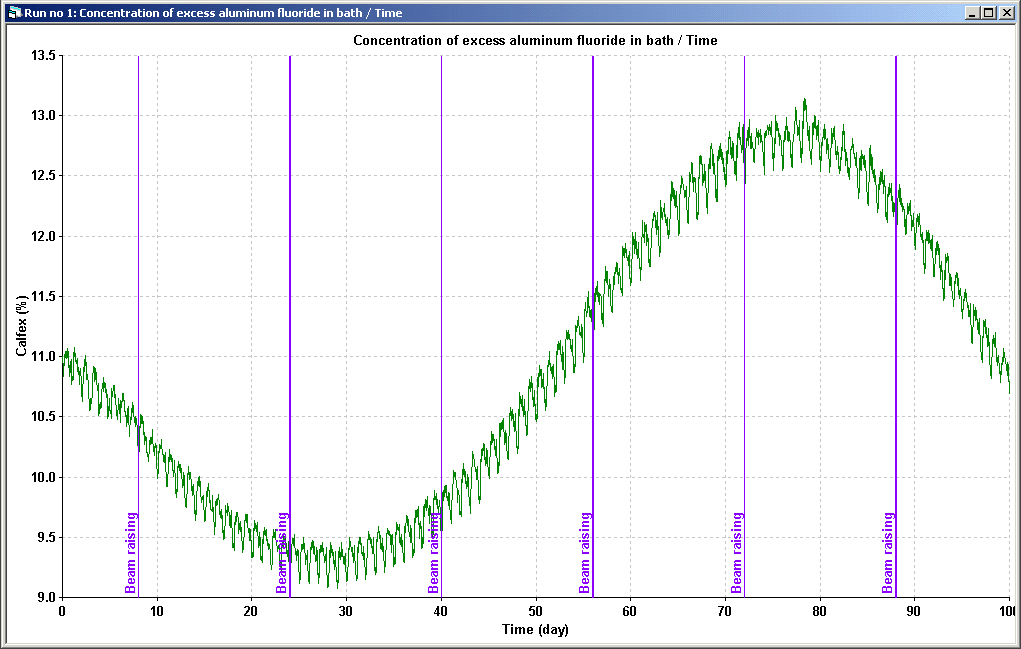
Figure 4: Operation with bath sampling every 3 days
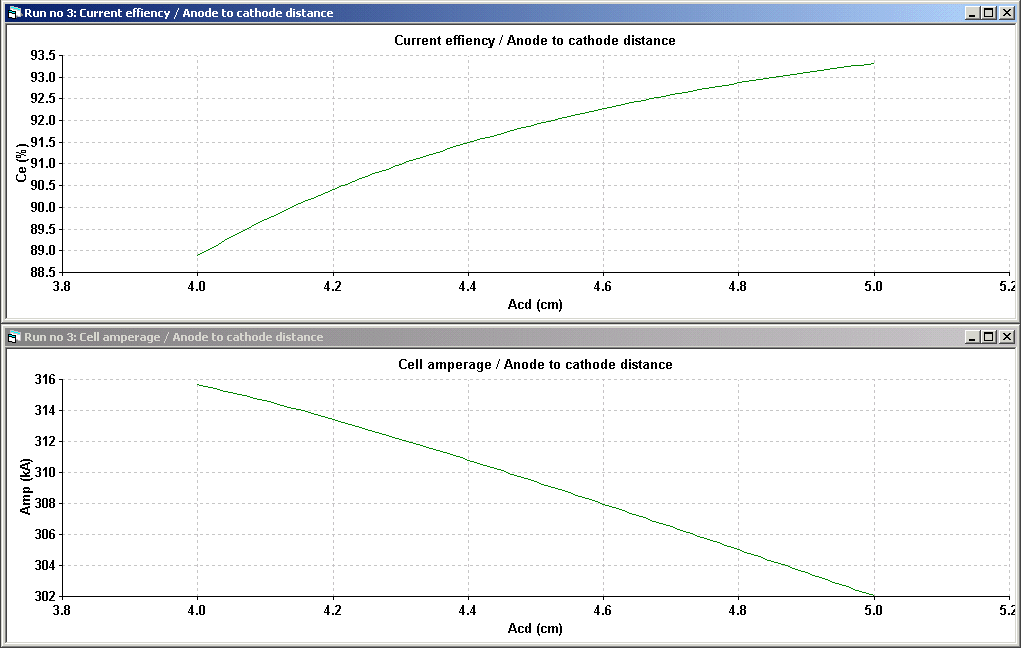
Figure 5: Impact of replacing ACD by Amperage at constant cell internal heat
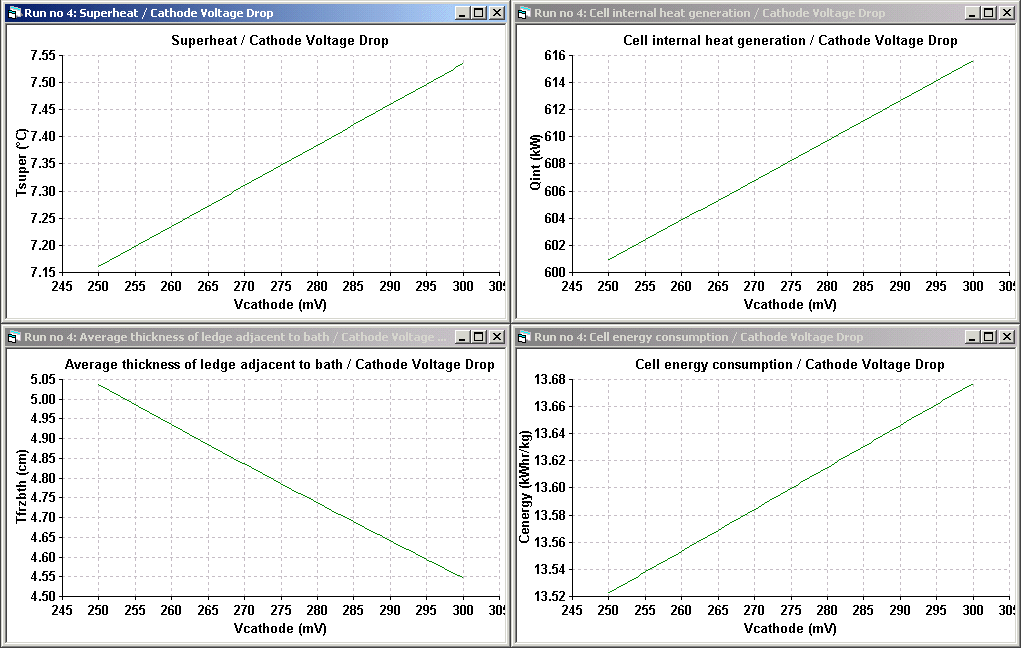
Figure 6: Impact of reducing cathode voltage drop at constant ACD
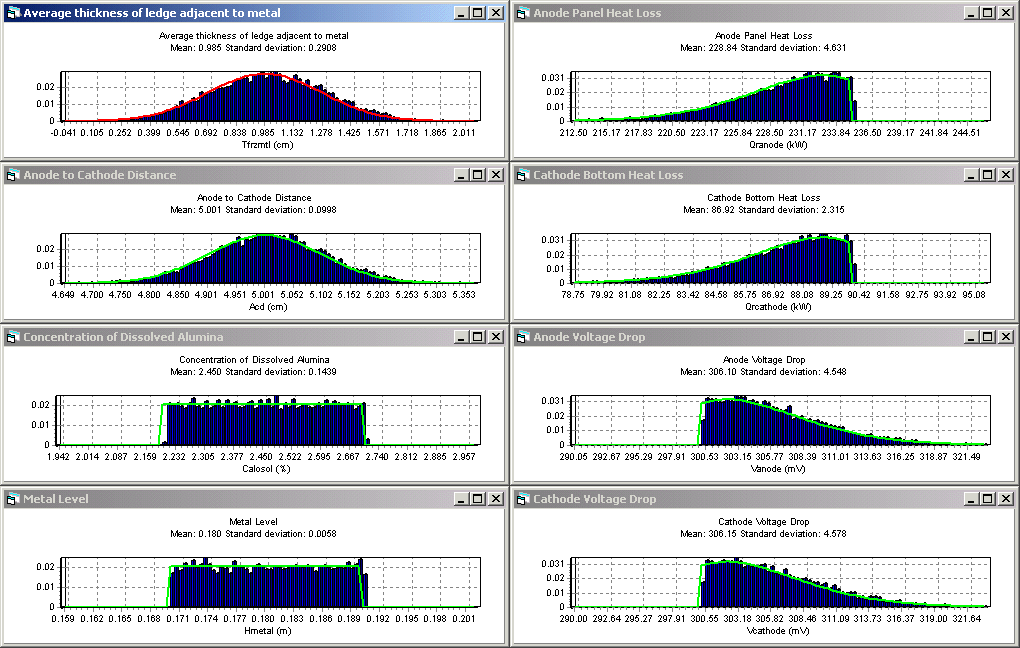
Figure 7: Monte Carlo risk assessment analysis
ANSYS-BASED 3D STEADY-STATE FINITE ELEMENT THERMO-ELECTRIC MODELS
ANSYS-based 3D thermo-electric steady-state models are used to find a detailed lining design that is compatible with the selected internal heat generation (which mostly depends on the selected anode current density and anode to cathode distance). It will predict the detailed ledge profile (variation of the ledge thickness) that corresponds to the required steady-state cell superheat once the cell internal heat and lining insulation characteristics have been selected.
As opposed to Dyna/Marc that is a single general purpose tool, ANSYS-based 3D thermo-electric models are specialized applications. Of course, they are all applications of ANSYS, a general purpose finite element commercial code; they also all rely on the same custom-made library of "APDL macros" wrote especially to streamline the development of such aluminium reduction cell thermo-electric models; yet, by nature, every ANSYS-based model is unique, so it is a set or collection of models:
| - | half-anode models (Figure 8) | |
| - | cathode side slice models (Figure 9) | |
| - | cathode end slice models | |
| - | cathode corner models (Figure 10) | |
| - | full cell side slice models (Figure 11) | |
| - | full cell quarter models (Figure 12) | |
| - | full half-cell plus busbars models (Figure 13) | |
| - | etc. |
Another way to classify them is by their type of cell technology. This is a partial list of models that have already been developed:
| - | Alcan A310 models | |
| - | Pechiney AP30 models | |
| - | Pechiney AP18 models | |
| - | Alcoa A697 models | |
| - | Alcoa P155 models | |
| - | Kaiser P69 models | |
| - | Reynolds P19 models |

Figure 8: Demo half anode model, temperature solution

Figure 9: Demo cathode side slice model, temperature solution
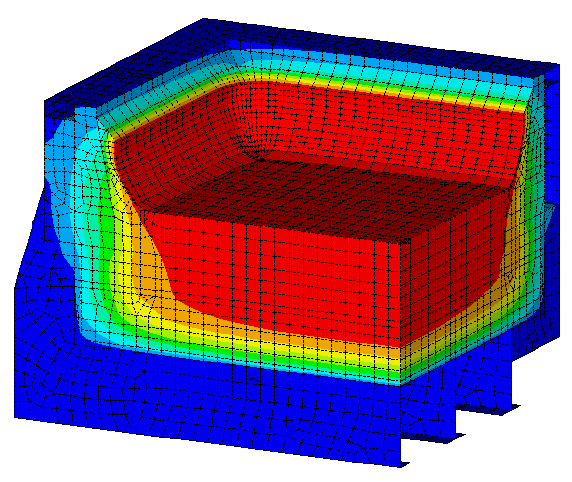
Figure 10: Demo cathode corner model, temperature solution
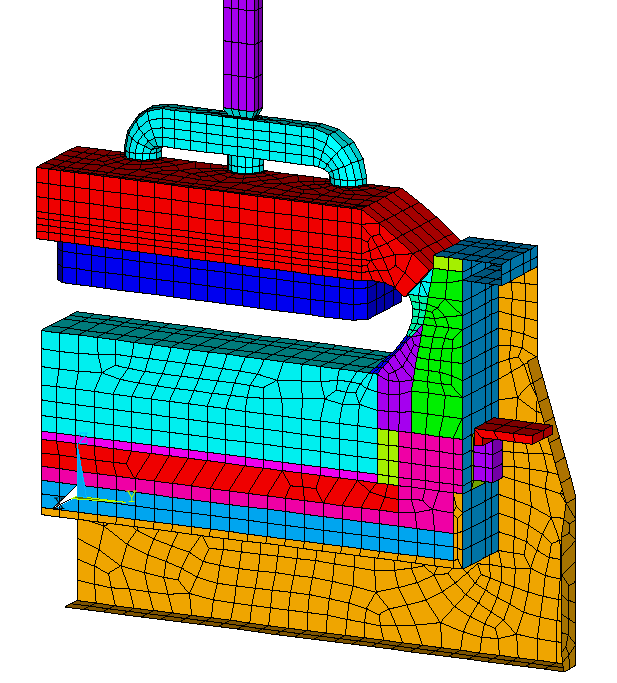
Figure 11: Demo full cell slice model, mesh

Figure 12: Demo full cell quarter model, temperature solution
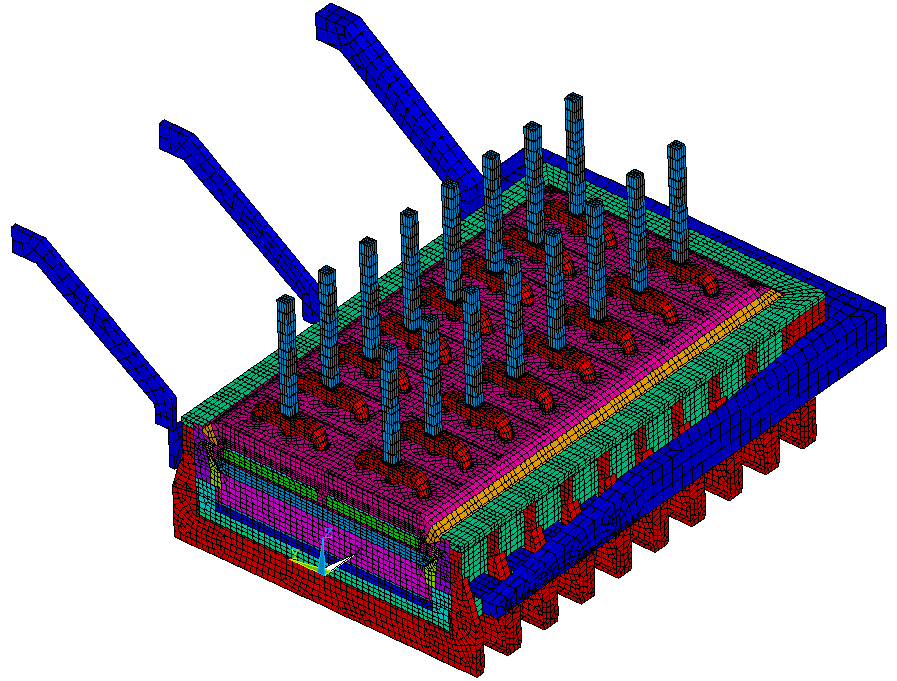
Figure 13: Demo full half-cell plus busbars model, mesh
What makes every ANSYS-based model unique is its topology, which is the mathematical description of its geometry. For example:
| - | prebaked anodes can have one, two, three, four or even six stud(s) |
| - | a single prebaked anode can be made of one or two carbon block(s) |
| - | cathode steel shells may be straight, have a step, a sloped side wall, a curved lower side wall or end wall; be orthotropic or have independent cradles |
| - | cathode blocks may have a single or a double bar(s) design; it may use split bars or not |
| - | cathode lining designs may have two, three, four or even five layers of different refractory and insulating materials under the cathode blocks |
| - | side blocks can be made of one, two or three material layer(s) vertically and one or two material layer(s) horizontally |
| - | the pier region could be make of firebricks, semi-insulating bricks, insulating bricks, castable refractory or any combination of the above; furthermore almost every pier shape design is unique. |
So because of the very wide variety of cell design, the topology of every cell design is unique, which means that every ANSYS-based 3D thermo-electric model must be custom-built accordingly.
On the other hand, one topology per model does not mean one geometry per model! Every topology can be "stretched" into an infinite number of geometries, for example:
| - | cathode block length and height can be changed | |
| - | collector bar length width and height can be changed | |
| - | cathode shell width and height can be changed | |
| - | etc. |
Each topology is described by a number of size parameters (cathode block length, collector bar height, etc.) and the value assigned to each parameter can be changed at will as long as those changes are topologically valid. For example, as the cathode blocks are placed inside a steel shell, the cathode block length must remain shorter than the shell width.
Another important feature of a model topology is that it is subdivided in regions (volumes in 3D space). Each region is then assigned to a material type and each material type is assigned to a set of non-linear (temperature dependent) material properties. So, it is quite easy to change, for example, the grade of the cathode block in the model. In such a case, only the set of non-linear material properties associated to the cathode block region has to be changed.
It is also possible to change the material type associated to a specific region from say firebrick to semi-insulating brick. Yet, most of the time, this kind of option must be planned ahead during the conception of the model topology, to allow only a part of the firebrick to be replaced by semi-insulating brick without having to create as many regions as there are individual firebricks in the lining!
Practically, this means for example that to have the option to replace a single material side block design by a two material side blocks design, two side blocks regions must be created in the model topology. To run the single material side block design, the same set of material properties are simply assign to the two regions.
CALIBRATION AND VALIDATION OF THE MATHEMATICAL MODELS
Even if it is based on a well established and already demonstrated to be reliable modeling technology, every new model must be validated before it could be considered reliable enough to be safely used in the context of a cell lining design retrofit study.
To be considered validated, a new model must be able to well reproduce the existing cell measured heat balance. So it is very important to have well established the existing cell heat balance. Typically, this is the most difficult part of the model development and validation exercise since obtaining reliable data of a cell heat balance from a thermal blitz campaign is a real challenge [8].
Once reliable heat balance data are available, it is relatively straightforward for an experienced modeler to calibrate the ANSYS-based mathematical models in order for them to well reproduce the measured behavior because those models are quite closely representing the physics and the geometry of the real problem. On the other hand, because Dyna/Marc models are based on major simplifications of the geometry of the problem, it is harder to calibrate them well. The most accurate and the most straightforward way to well calibrate a Dyna/Marc model is to use information obtained from a validated ANSYS-based 3D model.
EXAMPLES OF APPLICATIONS OF AN ANSYS-BASED 3D FULL CELL SIDE SLICE THERMO-ELECTRIC MODEL
Reference [7] presents a hypothetical retrofit study of a 300 kA, 13.75 kWh/kg cell into a 350 kA, 13.4 kWh/kg cell (similarly reference [9] presents the real story of the retrofit of the AP30 into the AP35 cell technology). In the hypothetical study, the cell internal heat was increased from 628 kW to 713 kW, so in this case, improving the thermal balance meant increasing it!
On the other hand, reference [10] presents another hypothetical retrofit study of the same 300 kA, 13.75 kWh/kg cell. This time, the cell is converted into a 265 kA, 11.94 kWh/kg cell. In the process of conversion, the cell internal heat was decreased to 427 kW. So this time, improving the thermal balance of the cell meant decreasing it!
Those two extreme cases clearly demonstrate that as far as the cell thermal balance is concerned, the window of opportunities is quite wide. Only a complimentary technico-economical study can indicate which of the two retrofit scenarios offers the best return on investment (obviously, the outcome of that study will mostly depend on the selected long-term cost of the electrical power).
CONCLUSIONS
These days, with the support of well established and reliable mathematical models, older smelters operating at 17-18 kWh/kg due to a poor thermal design should be able to come up with successful retrofit design proposal(s) well within a year, test that (those) design proposal(s) in prototypes during a minimum of two years and then be able to proceed to a full implementation phase. As far as the thermal balance problem of the cell is concerned, there is no known technical reason that should prevent a significant reduction of their power consumption.
REFERENCES