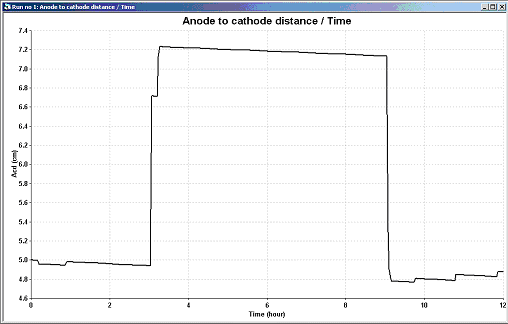
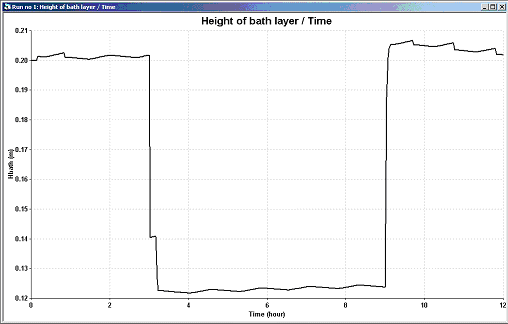
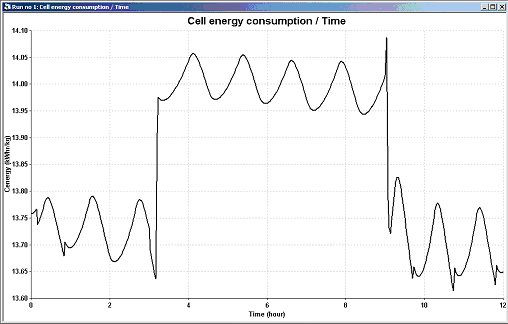
For that reason, a second model was developed following a "bottom up" approach, meaning that this time, the prime objective was to obtain fast answers. This model is based on the so-called "lump parameter" model concept [8,9].
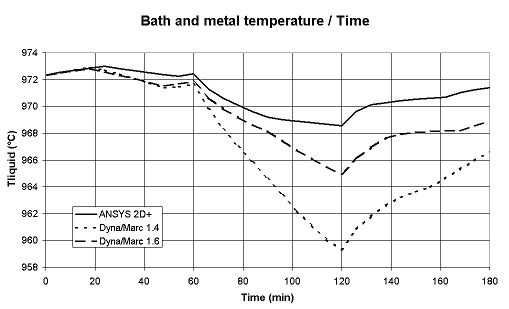
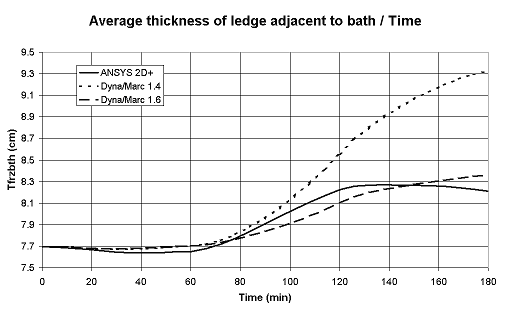
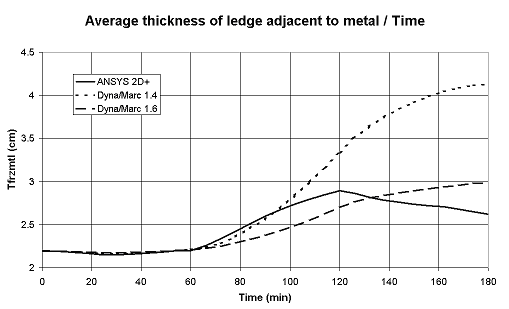
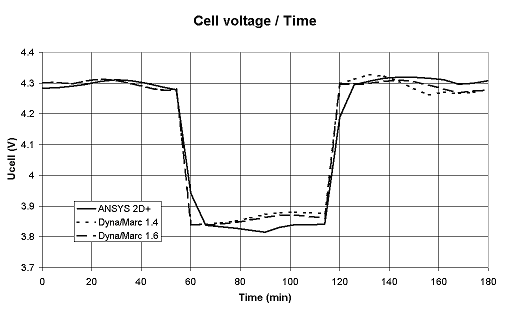
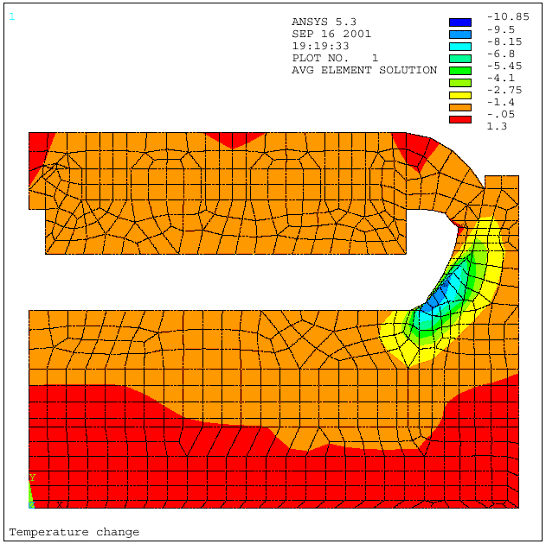
The original "lump parameter" model, as argued previously in [5] and illustrated in Figure 1, is accurate enough to be used to do fast analysis of the thermal response of a cell under normal operating conditions. But, as argued in [5] and illustrated in Figure 2, that model concept is not accurate enough to well represent the thermal response of a cell going through drastic exceptional events like a total power loss.
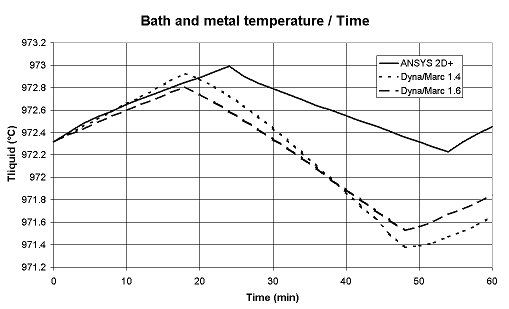
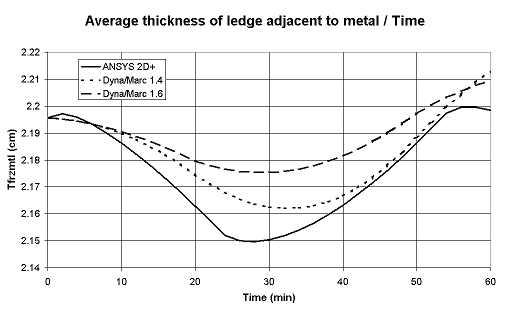
Figure 1: Normal operation
For that reason, the original "lump parameter" model had to be expanded to take into account the thermal response of the cell lining. That way, the model could be considered accurate enough to analyze the thermal response of power modulation events.
So an improved model has been developed and will be called a "lump parameter+" model. By definition, a "lump parameter" model is a 0D model. This means that no partial differential equations are used to solve thermal gradients like a 2D model does in 2 dimensions space or a 3D model does in 3 dimensions space.
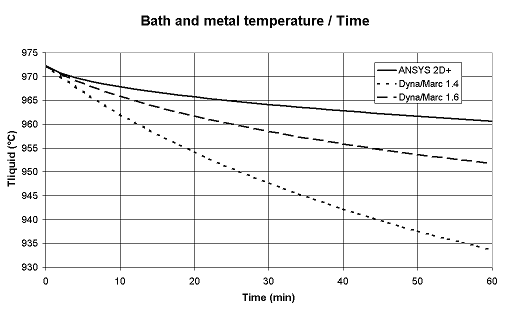
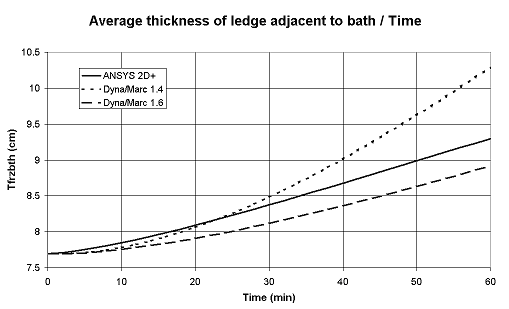
Figure 2: Total power failure
As the "+" in the 2D+ model stands for some crude representation of the third dimension in a 2D model [10], the "+" in the "lump parameter+" model stands for the addition of a 1D representation of the thermal diffusion in the anode and cathode panels as well as for the addition of a 1D representation of the thermal diffusion in the variable ledge thickness at bath and metal level [11].
This means that the "lump parameters+" model not only computes the thermal evolution of the lump mass of bath, metal and sludge, but also calculates the thermal gradients evolution in the anodes, the cathode blocks and the side ledge [12]. As seen in Figure 2, that improved model (denoted version 1.6) now reproduces fairly well the thermal response of a total power failure.
Still, the "lump parameter+" model computed the one hour thermal response in a fraction of second while the 2D+ model took 25 minutes wall clock time to compute it while running on a Pentium III, 800 MHz computer. Obviously, having access to both models is a tremendous advantage because, at the concept-screening phase of a project, speed is more important than accuracy while towards the end, accuracy becomes critical for fine-tuning the selected concept.