|
Abstract
Four fast algebraic models that respectively calculate the anode panel heat loss, the cathode bottom heat loss, the anode voltage drop and
the cathode voltage drop have been developed and incorporated into the Dyna/Marc 1.7 lump parameters+ cell simulator. The results from
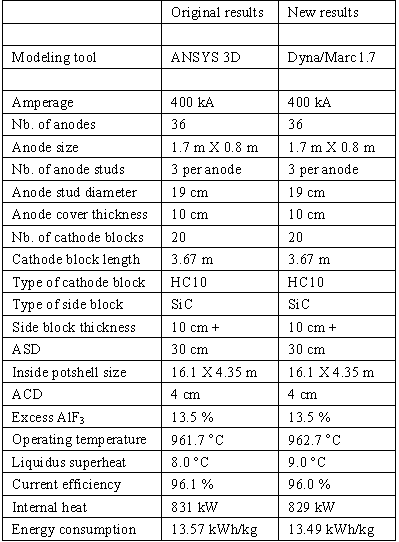
Dyna/Marc 1.7 are compared with results from more complex ANSYS® based 3D thermo-electric finite element models.
With the addition of these four algebraic models to the lump parameters+ cell simulator, it is now possible to perform fast trend analysis
of key design parameters like the anode stud diameter, the stud hole depth, the collector bar size or the type or grade of cathode block.
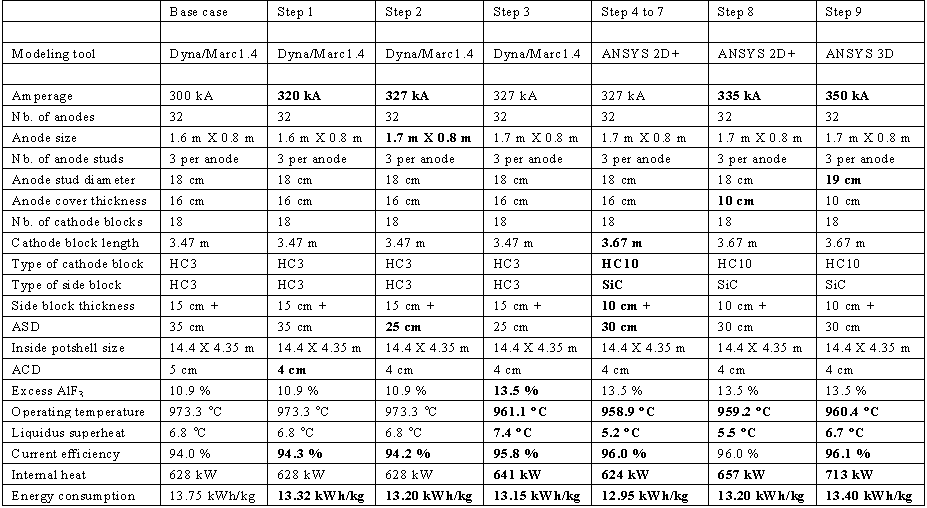
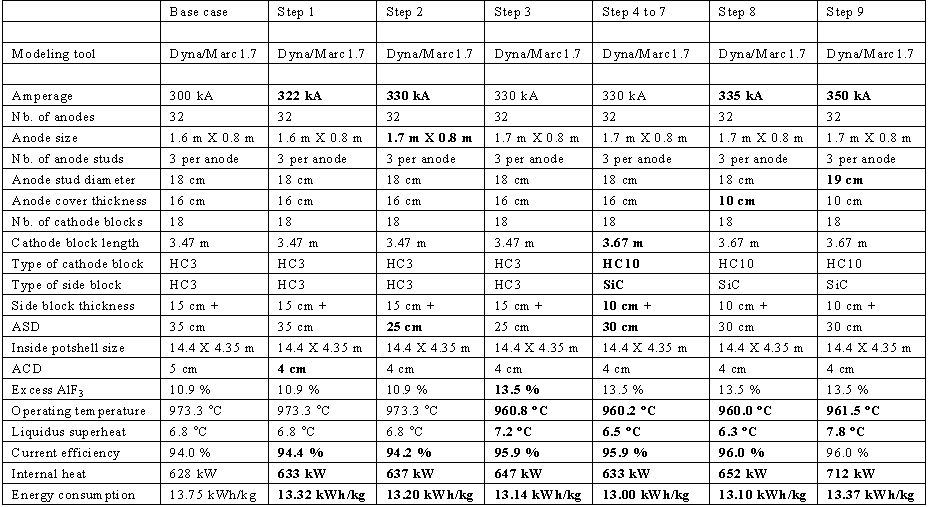
In order to illustrate the increased power of the lump parameters+ cell simulator as a brainstorming session "what if" tool, the previously
published retrofit study of a 300 kA cell into a 350 kA cell was repeated, this time using only the lump parameters+ cell simulator as
modeling tool.
Introduction
It is important to well understand the physics of the heat dissipation inside the lining of an aluminum reduction cell to be able to
represent it properly in a mathematical model.
The key feature to be represented accurately is the 2 zones heat loss mechanism [1,2]. In one zone, the driving force is the global
thermal gradient between the cell operating temperature and the cell ambient temperature. In the other zone, the driving force is the
cell superheat!
3D finite element based thermo-electric models that are converging the ledge profile as part of the solution [3] reproduce very well
that dual zones heat loss mechanism as well as the complex geometry of the cell. Unfortunately, they are too time-consuming to be used
efficiently in a brainstorming session at the beginning of a cell retrofit project. They cannot provide fast answers to "what if"
questions raised during these meetings.
|
|
2D+ finite element based [3,4] or 2D finite difference based [5] models converging the ledge profile also represent well the dual zones
of heat loss and, at the same time, represent fairly well the cell's complex geometry. These days, computers are fast enough for these
models to provide an answer to brainstorming "what if" questions in a matter of minutes. This would be fast enough to answer a few
questions but having to wait often for the answers of multiple questions will definitely break the rhythm of the meeting!
The last option would be to use a lump parameter+ model [4,6]. This is the simplest possible model that still represents the two zones
heat dissipation of the cell. This model is so simple, that you can get answers to "what if" questions in a fraction of second.
Nevertheless, as demonstrated in [7,8], the accuracy of the lump parameters+ model predictions are surprisingly accurate considering
its simplicity.
Unfortunately, up to now, the lump parameters+ model was so simple that it could not assess the impact of changes of such basic design
parameters as the anode stud diameter or the cross section of the collector bar on the cell heat balance. This meant that its utility
as a stand-alone modeling tool in a brainstorming session was limited.
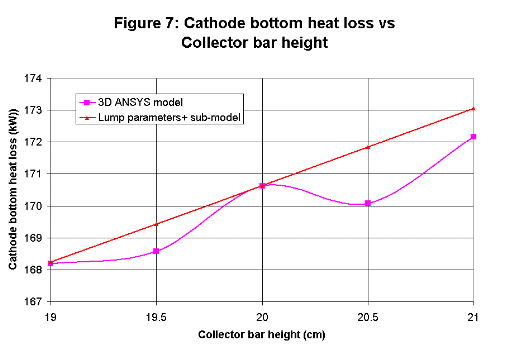
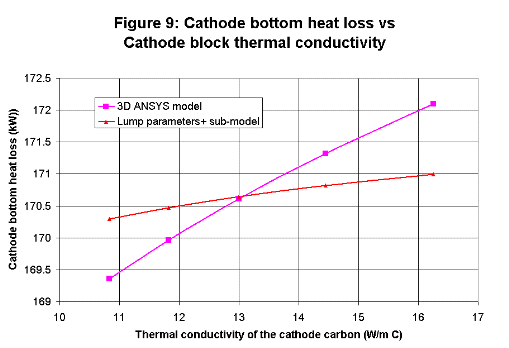
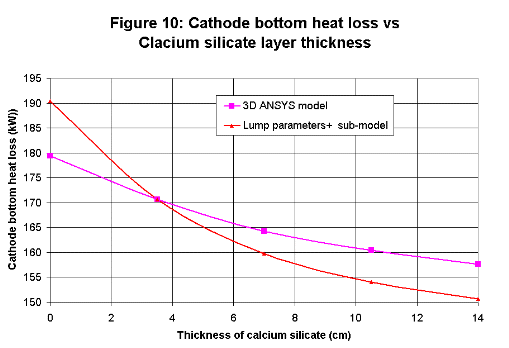
For that reason, the original lump parameters+ model has been expanded by adding to it four new algebraic sub-models that respectively
calculate the anode panel heat loss, the cathode bottom heat loss, the anode voltage drop and the cathode voltage drop. Those new
algebraic sub-models are based mainly on correlations developed in the late 1950's [5] when using complex mathematical models to design
a cell was clearly not an option!
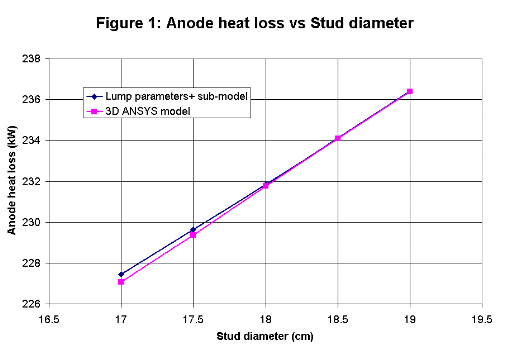
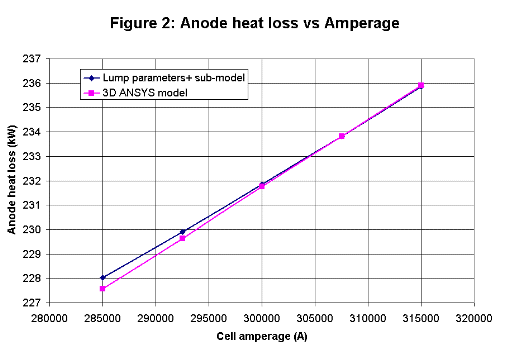
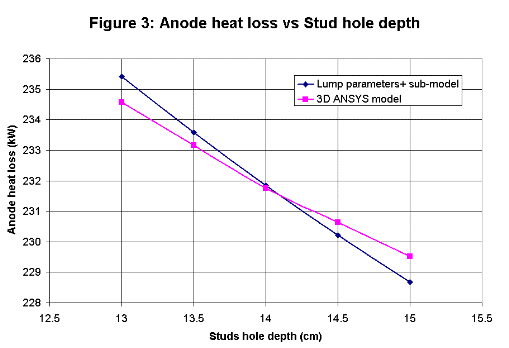
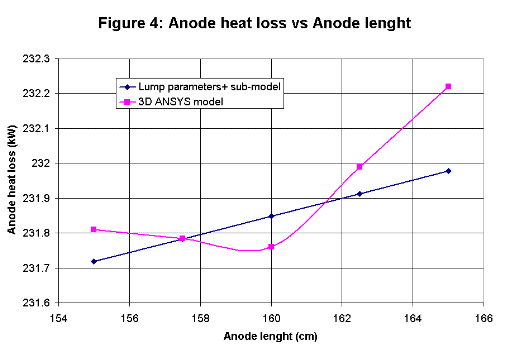
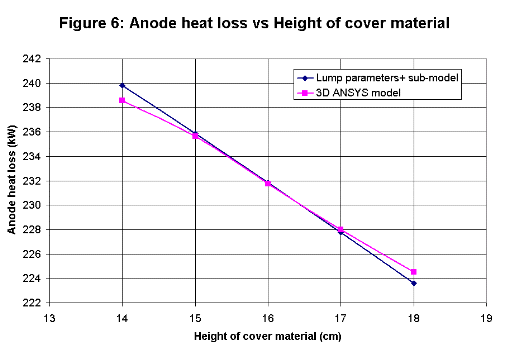
Anode panel heat loss sub-model
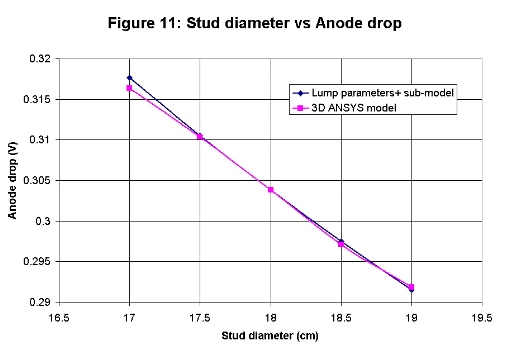
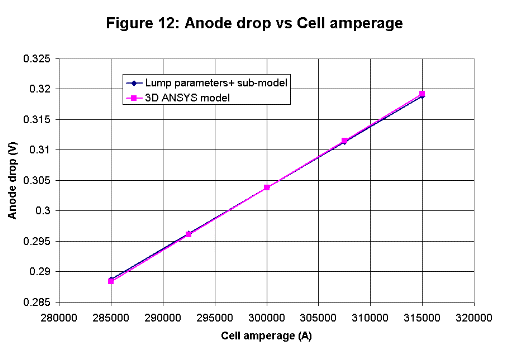
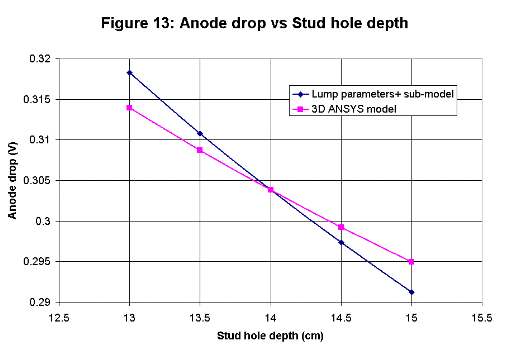
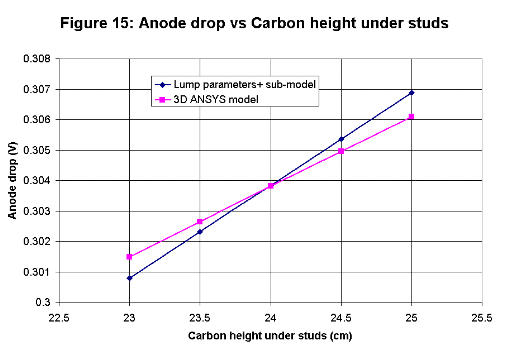
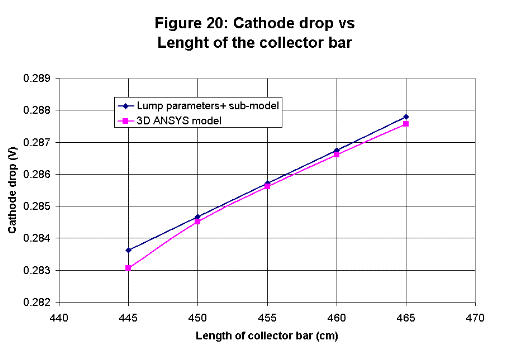
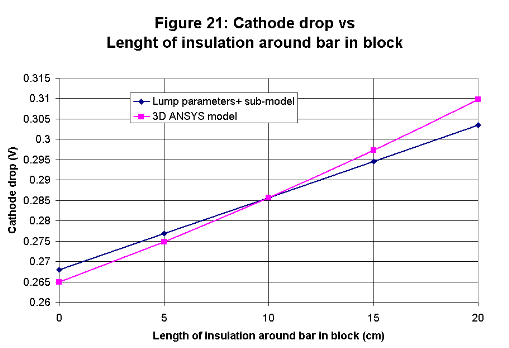
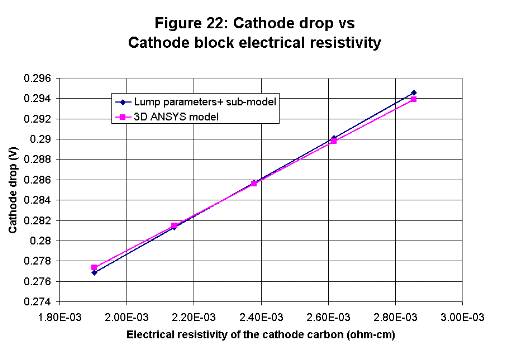
All four new algebraic sub-models are based on semi-empirical correlations. The initial work done in the 1950's was based on correlations
with measurements while the recent development is rather based on correlations with 3D ANSYS® model results.
|