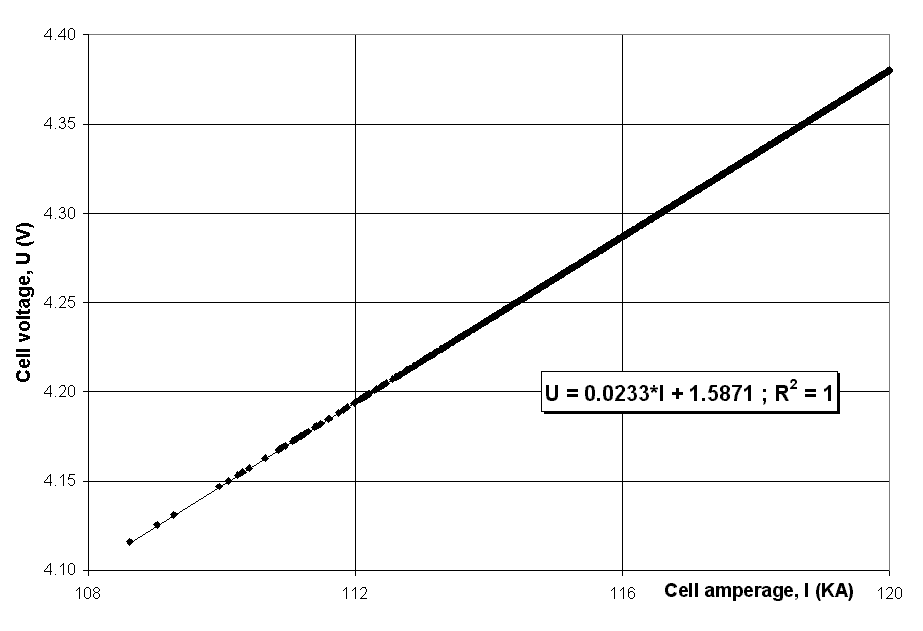
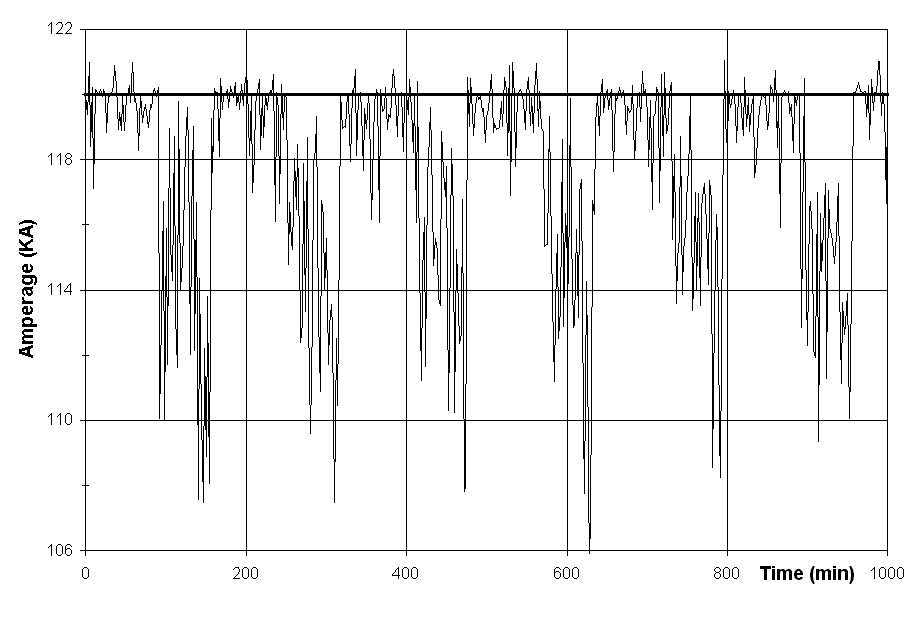
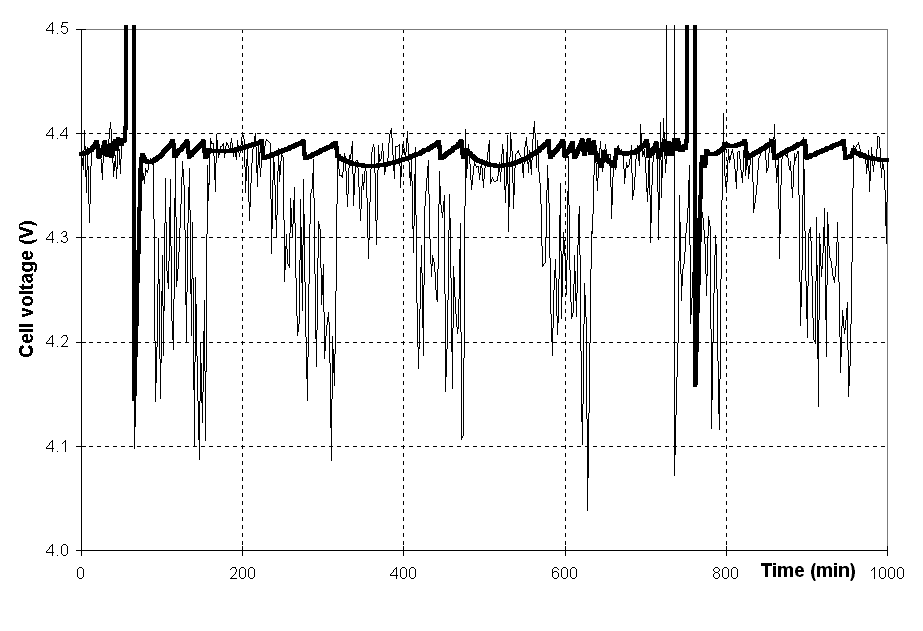
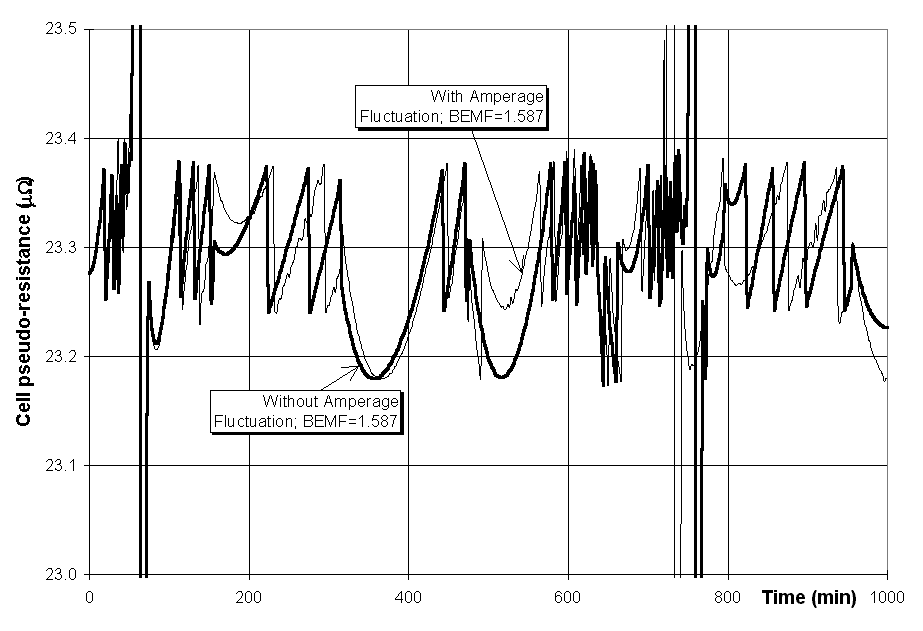
cell voltage. Since the cell voltage was found to vary linearly with amperage, the cell pseudo-resistance (R) is computed as follows:
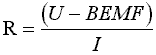 (1)
(1)
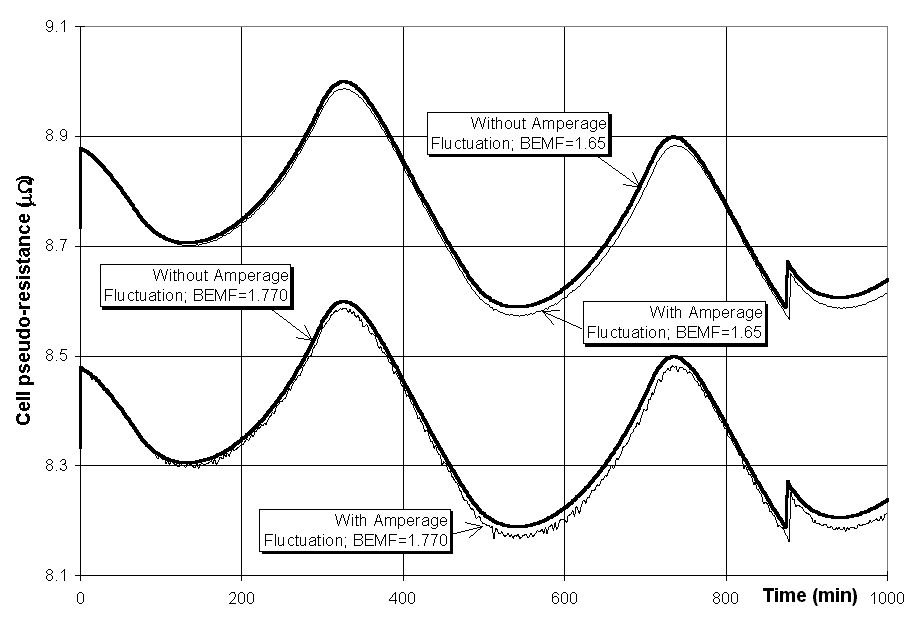
where U is the cell voltage, I is the line amperage and BEMF is referred to as the back electro-motive force. BEMF is really the zero current intercept of the tangent to the cell voltage vs. cell amperage curve at the point of nominal cell operation. By definition, R should not be affected by the fluctuation in the line amperage.
Factors Affecting the BMF
An evaluation of the factors that affect the BEMF requires a close look at the cell voltage since the BEMF is calculated based on the slope of the voltage versus cell amperage curve. The cell voltage (Ucell) is defined as:
Ucell=Ubath+Uelec+Uext+ Uand+Ucath (2)
where
| Ubath | Voltage drop in the bath; | |
| Uelec | Electrolysis voltage; | |
| Uext | Average voltage drop in the external busbars; | |
| Uand | Anode mid life average voltage drop; | |
| Ucath | Cathode average voltage drop at a given life. |
The bath voltage is a function of the bath resistivity and the voltage drop in the bubble layer below the anodes. Models of the bath resistivity have been published in the literature [3,4]. It is a function of the bath ratio, concentration of alumina and other additives in the bath, and the operating temperature. Haupin [5] expressed the bubble layer voltage as a function of the current density, bath resistance, alumina concentration and the thickness of the bubble layer. Welch [5] proposed a simpler model which expressed the bubble voltage as a function of the bath resistivity, anode current density, the thickness of the bubble layer and the gas fraction in the layer.
The electrolysis voltage is characterized by four components namely the reversible (equilibrium) voltage, concentration overvoltage at the cathode, reaction overvoltage at the anode and concentration overvoltage at the anode. The components are represented by complex semi-empirical expressions and the reader is referred to the literature for more details [5,6]. The expressions are a function of the current density, bath ratio, alumina concentration and the operating temperature [7,8].
The cathode, anode and external voltage are dictated by the cell design and the busbar configuration. Depending on the desired accuracy, they can be calculated using a simplified network analysis or detailed finite element thermo-electric models [9].
It is clear from the above that several factors affect the cell voltage and hence the BEMF. The anode and cathode current density play a major role. They are a function of the cell amperage as well as the anode geometry and the freeze profile the later being highly dependent on the cell operation. Two other important factors are the operating temperature and the alumina concentration in the bath.
The BEMF is often assumed to be constant with different values quoted in different sources (1.62-1.68 V in reference [6] 1.6-1.8 V in reference [10]). A value of 1.65 is often chosen. It is common practice within each smelter to calculate a value of BEMF from the recorded line amperage and cell voltage.
Two examples, a PBF and a side break cell design, will be used to study the values of BEMF and evaluate the effect of its accuracy on the pot behavior.
PBF Cell Operating at 300 kA
As a first case study let us use the PBF prototype cell operating at 300 kA presented in an article in the February 1994 issue of JOM [10]. First, we can use the Monte Carlo mode of the steady state solver to study the impact of the amperage decrease on the cell voltage at constant ACD and cell temperature. To do this, the metal level was selected as the target variable. The metal level is calculated that would allow the cell heat loss to remain equal to the internal heat as the amperage is decreased.
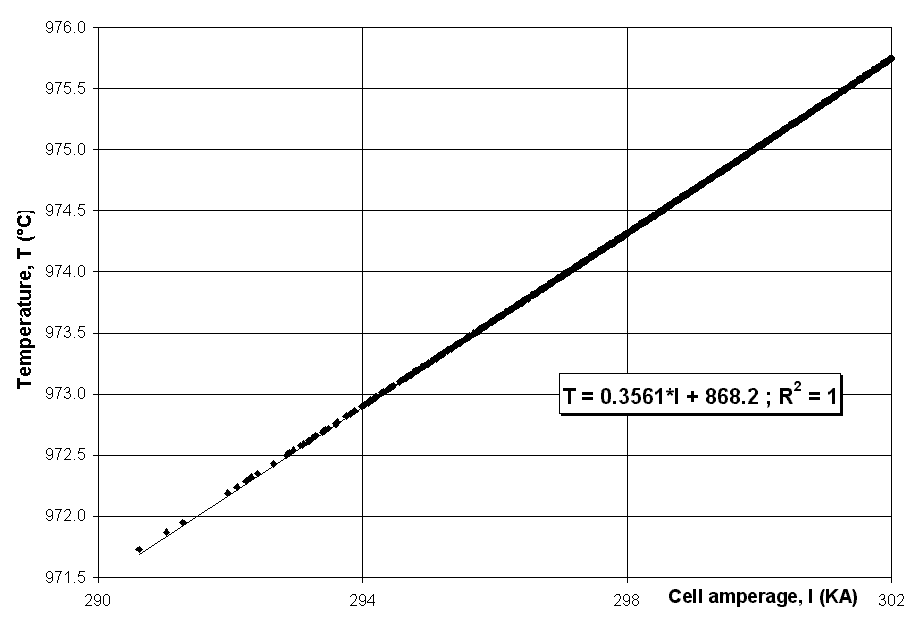
As we can see in Figure 1, for this particular cell design, the zero current intercept or BEMF is equal to 1.632V.
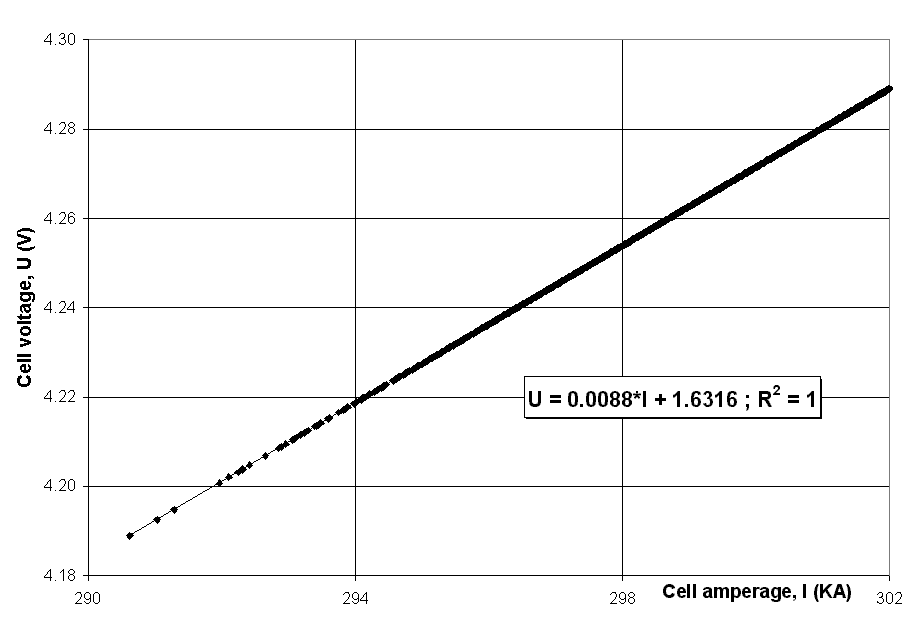
Figure 1 - Correlation between the cell amperage and the cell voltage (PBF cell with the metal height as the target variable).
To help illustrate the sensitivity of the value of the BEMF, let us change the setup of the steady state Monte Carlo solution. This time we will keep the ACD constant, but we will select the temperature as the target variable to converge the heat balance as the amperage decreases.
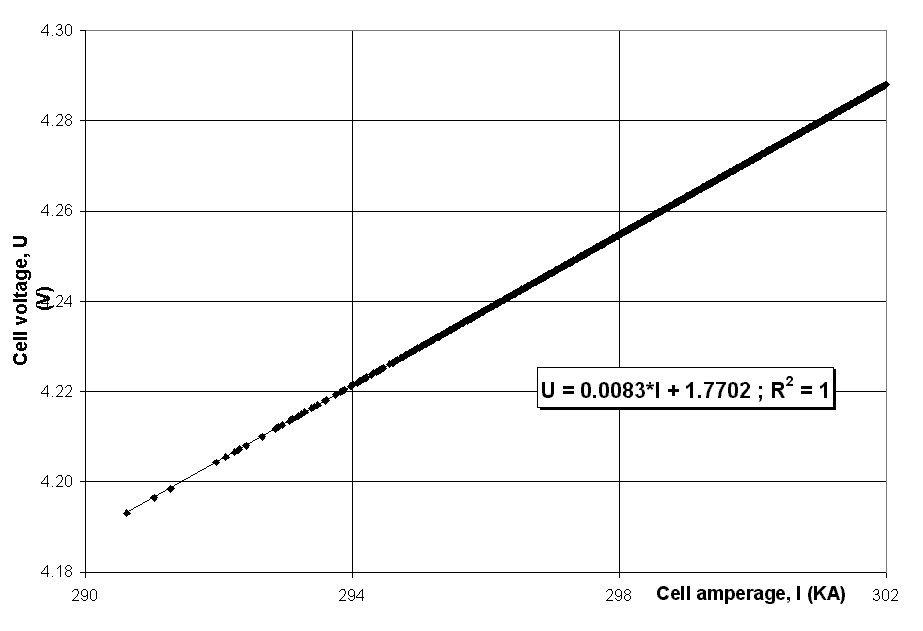
Figure 2 - Correlation between the cell amperage and the cell voltage (PBF cell with the cell temperature as the target variable).
With this setup, the value of the zero current intercept is increased to 1.770V (see figure 2). A decrease in temperature, as shown in figure 3, will cause an increase in the bath resistivity and hence an increase in the cell voltage. This increase is offset by the reduction in voltage due to the